Jobineries

Les casse-tête sudoku sont extrêmement populaires par les temps qui courent. J'aimerais cependant attirer votre attention sur un autre type d'énigmes qui, ma foi, existent depuis une bonne dizaine d'année.

En américain, on les appelle des cross sums. Vous en trouverez plus de vingt (du plus facile au plus difficile) à chaque parution du magazine Dell Math Puzzles and Logic Problems. Ci-dessous, le problème no. 13 de l'édition du mois de novembre. (Désolé pour la numérisation. Je crois cependant que l'image est suffisamment claire pour vous donner une bonne idée du problème.)



Les règles sont simples :
1. Vous devez remplir les espaces blancs par un chiffre de 1 à 9.
2. Chaque combinaison de chiffres doit s'additionner pour donner le résultat à gauche pour une combinaison horizontale et au-dessus pour une combinaison verticale.
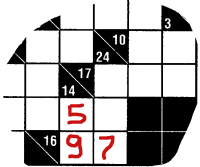3. Vous ne pouvez réutiliser le même chiffre dans une même combinaison. Par exemple, si vous devez trouver deux chiffres qui donnent 16, (comme en bas et à droite de l'image), vous pouvez inscrire soit 7 et 9, ou 9 et 7, mais non 8 et 8. Donc, la seule combinaison possible (pour le 16 qui est en bas et à droite de l'image) est 9 et 7, car si on mettait 7 et 9, on ne pourrait compléter la somme verticale qui doit donner 14, car cela impliquerait une combinaison de 7 et 7.

Les cases entourées de gris vers le centre de la grille n'ont pas d'importance. Elles entourent une combinaison donnée un peu plus loin dans le magazine pour aider ceux qui en ressentent le besoin.

J'ai bien souri en lisant la citation ci-dessous trouvée dans un commentaire de François Guité sur son blogue.

La technologie est dominée par deux types de personnes : ceux qui comprennent ce qu’ils n’administrent pas, et ceux qui administrent ce qu’ils ne comprennent pas.

Reconnaissant le style loi de Murphy, j'ai tenté une petite recherche sur le web. Ici, on trouve quelques explications. De là, un très beau néologisme anglais fait surface : Teachnology. Voir http://www.teachnology.org.

Sous Archibald Putt, dans Wikipédia (en), on apprend que l'aphorisme originerait du «Research/Development magazine» de janvier 1976.

Deux livres éloignés de 50 ans et lus dans un même intervalle de temps. Deux idées soeurs :

Prenez un homme qui a construit une grande oeuvre et dont le nom est célèbre dans les sciences, les arts ou les lettres. Il a fort peu de chances d'être agréé par les électeurs. Ni Pasteur ni Renan ne réussirent à obtenir un mandat.
Louis Latzarus, La Politique, Librairie Hachette, 1928

Au Québec, terre d'Amérique, il ne nous vient pas à l'esprit qu'un chef d'État puisse être en même temps un poète, un philosophe, un musicien. Si, par aventure, un tempérament d'artiste voulait arriver au pouvoir, il devrait, pour ne pas détériorer son image, camoufler cette «tare». Aussi ne faut-il pas s'étonner que nous n'ayons jamais eu d'hommes politiques imaginatifs, capables d'insuffler à la nation un idéal de l'esprit.
Albert Brie, Le mot du silencieux, Fides, 1978.

On ira sans doute aux urnes en janvier. Je penserai à ces deux citations lorsque viendra le moment de mettre mon «X».

Très intéressant le roman Un soir au club de Christian Gailly. Son personnage central est un retraité du jazz (et de la boisson) depuis 10 ans. Mais une courte visite à un club, jumelée à un accident opportun changera sa vie. Sommes-nous toujours le même? Voilà une question à laquelle Gailly, subrepticement, s'attaque.

J'ai toujours de la difficulté à entendre du Jazz. J'ai beau parfois écouter les émissions de Péan ou de Vigeant à Radio-Canada, je demeure avec une grande incompréhension du genre. Un passage dans le Gailly vient peut-être m'expliquer mon malaise :

«Or dans le jazz il n'y a pas de beauté. Du swing, certes, de l'émotion, de la joie et de la danse dans le corps, voire de la rage, tristesse ou gaîté mais pas de beauté, je regrette.» (p.119)

En écoutant du Bach, du Handel ou du Scarlatti, je vibre toujours à cette beauté musicale. Sans doute recherchais-je une semblable esthétique dans le jazz, alors que la quête devrait peut-être s'orienter dans une tout autre direction.

Vous trouverez ici l'origine du mot diariste. De là, il n'y a qu'un pas vers le néologisme cyberdiariste. Dommage que ce mot soit si près d'un autre qui invariablement amènera la réflexion suivant : un blogue ne serait-il qu'une diarrhée cybernétique?

« L'intentionalité n'est qu'une propriété que l'esprit prête aux objets dans l'objectif de les simuler efficacement. C'est l'évolution qui nous a conduit à catégoriser différemment les êtres vivants et les non-vivants parce qu'ils ne se simulent pas efficacement de la même manière.
Ce qu'a compris Spinoza c'est que les deux ne font qu'un et que tout fonctionne par l'enchainement des causes matérielles. »
Arnaud Megret

Citation du jour sur le site de la Société Francophone de Mémétique.

Saviez-vous que le 31 décembre qui vient, on devra ajouter une seconde intercalaire à notre montre ?

Bobin mène sa carrière d'écrivain loin des feux de la rampe. Je ne crois pas qu'il ait été nominé pour un prix littéraire quelconque. Mais qu'en aurait-il à en faire, de ce prix? Il possède son lot de lecteurs indéfectibles (dont je fais partie) et cela doit lui être bien suffisant. Toujours est-il qu'il vient de publier un beau petit livre ayant pour thème sa «relation» avec son Creusot natal. Prisonnier au berceau est agrémenté de plus d'une vingtaine de photos ou d'images noir et blanc.

Les lecteurs d'Au fil de mes lectures savent combien j'affectionne Bobin. C'est un poète de l'intériorité, de la lumière, de la beauté. Comment, par exemple, ne pas apprécier un auteur qui nous lance des phrases du genre «[...] rien ne sera jamais aussi vaste qu'un visage ouvert par l'étonnement d'aimer.» Plus loin, une anecdote avec son père : «Quand il me vit, d'abord il ne me reconnut pas. [Son père était atteint de la maladie d'Elzeimer -GGJ] Puis le crêpe de la maladie s'enflamma, ses yeux s'ouvrirent sur moi, son soulagement rajeunit ses traits et il avait un visage d'enfant crédule quand il me demanda : "Comment as-tu fait pour me retrouver?" Cette parole, je l'entends chaque fois que je rencontre vraiment quelqu'un.»

Le message de Chistian Bobin est complexe de simplicité : Le paradis c'est d'être là...

Liane : Le livre chez Mercure de France.

Je viens tout juste de lire ce passage dans Cyberpresse | Actualités. C'est la ministre Forget qui parle.

«Alors, moi, je sais qu'aujourd'hui il y a 175 000 enfants qui ne sont pas à l'école, il y a donc 175 000 familles qui sont touchées.» Le paragraphe plus bas, le journaliste écrit : « La ministre a évalué qu'il y a eu plus d'un million de jours où les parents ont dû intervenir puis trouver quelqu'un (pour garder leurs enfants).»

Donc, si je saisis bien, notre bonne ministre pense qu'une famille québécoise n'a qu'un seul enfant....
Un million de jours, c'est tout près de 2739 ans... Cela veut-il dire que depuis le début des grèves rotatives, les parents québécois ont dû intervenir l'équivalent de 2739 ans pour résoudre les problèmes de garderie ?
Madame Forget est présidente du Conseil du Trésor. En tout cas, si j'avais un trésor, ce n'est pas à elle que je le confierais. J'ai beaucoup de difficulté à prendre cette femme au sérieux...

Un roman bizarre que Dans la luge d'Arthur Schopenhauer. Quatre personnages prennent la parole. Un philosophe spécialiste de Spinoza mais qui abandonne complètement son maître à penser (ou ne serait-ce plutôt Spinoza qui abandonne son disciple?), sombrant ainsi dans une profonde dépression. Il y a aussi sa femme, qui ne semble pas plus équilibrée que son mari. Un ami qui écoute et raconte. Il dira d'ailleurs : « Beaucoup de choses peuvent avoir du sens et de la pertinence, c'est la vie qui n'en a pas, le tout n'a aucun sens mais chacune des parties en a. » Enfin, la psychiatre qui prendra la parole au dernier chapitre. Le tout, ma foi, dans un décousu assez sympathique.

Le style est très près de celui de Thomas Bernhard. Un exemple vous convaincra : « [...] pendant des années nous avions Spinoza, Spinoza! pan! pan! pan! aujourd'hui exaltations diverses, drogues et main molle. La folie n'excuse pas tout. La vie conjugale nous a tués, comme elle tue tout le monde, et ce n'est pas la philosophie croyez-moi qui vous donne un coup de main dans la vie conjugale, d'ailleurs je ne vois rien qui puisse vous sortir la tête de cette embarcation maudite, surtout pas la philosophie qui en gros, sous des allures plus ou moins provocantes, s'est toujours attachée à calmer les esprits, à réduire la bête sauvage, notre meilleure part [...] »

De plus, on retrouve ici le thème de Maîtres Anciens de Bernhard : l'abandon des «Maîtres» lorsqu'un coup dur frappe.

Bon livre? Bof, qui suis-je pour en juger? Pour moi, un livre fait son boulot lorsqu'il me donne un bon moment de lecture. Et ce livre a rempli ce travail. Voilà pourquoi je me laisserai sans doute séduire par au moins un autre Reza.

Jubilatoire, ce roman de Vita Sackville-West (1892-1962). D'abord publié en 1931, il raconte l'histoire de lady Slane, 88 ans, qui vient de perdre son vieux mari. Après toute une vie consacrée à ce dernier, elle décide enfin de vivre la sienne. Elle quitte sa demeure de toujours pour se réfugier dans une petite maison, loin des tracas familiaux. Libre, lady Slane se fera de nouveaux amis dont l'un lancera la tirade suivante :

« [...] j'ai horreur de tous ceux qui ne voient pas le monde comme il est. C'est-à-dire monstrueux, lady Slane ! Et monstrueux parce qu'il est construit sur la compétition, sans que personne ne sache si la raison fondamentale de cette compétition est une pure convention ou une nécessité, une extraordinaire illusion, une loi naturelle ou animale destinée à disparaître à mesure que nous progressons dans la civilisation. Je crois que l'homme a construit sa vie sur un système mathématique erroné. Certes, il s'est arrangé pour que ses calculs tombent juste, parce qu'il a forcé le monde à accepter ses hypothèses. Mais si l'on choisissait de raisonner autrement, la réponse serait peut-être identique et ces hypothèses de départ apparaîtraient délirantes, astucieuses sans doute mais délirantes. Peut-être qu'un jour une authentique civilisation viendra corriger nos erreurs présentes? Mais nous avons encore du chemin à faire, oui, la route sera longue... » (p. 62)

Un excellent livre sur la beauté de la vieillesse.

Il y a certainement un concours dans l'air : j'ai reçu une dizaine de courriels dans lesquels on me demande l'auteur de la citation suivante :

«Il faut en finir avec cette légende du siècle dernier qui veut qu'au paradis on s'ennuie à mourir, et que l'enfer soit peuplé de gens intéressants et célèbres.»

Il paraît que la réponse se trouve parmi les trois possibilités suivantes :

• Sacha Guitry
• Nina Berberova
• Philippe Sollers

Malheureusement, toutes mes recherches sont restées infructueuses... Mais en fouillant, je suis tombé sur ce joli proverbe arabe : « Le paradis de la terre se trouve entre les seins d'une femme, sur le dos d'un cheval, dans les pages d'un livre. »