La mathématique présentée à la manière euclidienne apparaît comme une science systématique, déductive ; mais la mathématique en voie de formation se présente comme une science expérimentale, inductive.
G. Pólya
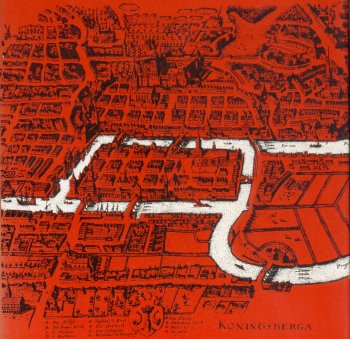
« À Kœnigsberg, en Poméranie, il y a une île appelée Kneiphof; le fleuve qui l'entoure se divise en deux bras, sur lesquels sont jetés les sept ponts a, b, c, d, e, f, g. Cela posé, peut-on arranger son parcours de telle sorte que l'on passe sur chaque pont, et que l'on ne puisse y passer qu'une seule fois? Cela semble possible, disent les uns; impossible, disent les autres. »
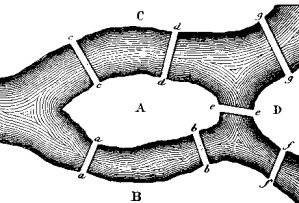
C'est ainsi que commence un fameux Mémoire d'Euler :
Solution problematis ad Geometriam situs pertinentis (1736). La solution d'Euler est d'une très grande beauté. Évidemment, dans son Mémoire, Euler généralise sa solution au problème. Je me contenterai ici d'utiliser sa méthode pour résoudre le problème précis des ponts de Kœnigsberg.
1. Euler commence d'abord par schématiser le problème.
2. Il indique qu'on pourrait le résoudre
«en faisant l'énumération complète de tous les parcours possibles; on reconnaîtrait ainsi s'il existe ou non un chemin qui réponde à la question.» Euler, rejette cette manière, car il désire aussi une solution qui s'appliquerait à plusieurs situations du même genre. De plus, il signale «
qu'après avoir terminé l'opération on aurait rencontré un grand nombre de choses qui ne sont pas en question; c'est en cela, sans aucun doute, que réside la cause d'une aussi grande difficulté.»
3. Euler indique par A, B, C, D les quatre régions séparées par les bras du fleuve :
« [...] si on passe de la région A dans la région B, soit par le pont a, soit par le pont b, je désigne ce chemin par AB. Maintenant si le voyageur passe de la région B à la région D, par le pont f par exemple, je désigne la seconde traversée par BD, et l'ensemble des deux passages par ABD; ainsi, la lettre intermédiaire B désigne en même temps la région d'arrivée après la première traversée, et la région de départ pour la seconde.»
4. Euler tire de cette notation une première conclusion : si on passe
un pont, le trajet aura
deux lettres. Si on passe
deux ponts, le trajet aura
trois lettres, etc. Dans notre problème particulier, le trajet ainsi noté aura donc
huit lettres, puisqu’'on désire passer une et une seule fois sur les sept ponts. (Euler généralise en disant que pour
n ponts, on aura
(n+1) lettres.
5. Euler observe ensuite que si 1 pont mène à une région, la lettre de cette région apparaîtra une seule fois dans le parcours. Si 3 ponts y mènent, la lettre apparaîtra 2 fois (soit qu'au début on parte de cette région ou d'une autre quelconque.) Si 5 ponts y mènent, la lettre apparaîtra 3 fois. Encore une fois, dans son Mémoire, Euler généralise en disant que si le nombre de ponts est
2n + 1 (un nombre impair), alors le nombre de lettres de la région est
n + 1.
6. Dans le cas de Koenigsberg, en franchissant tous le ponts :
Région A, 5 ponts, la lettre doit apparaître 3 fois.
Région B, 3 ponts, la lettre doit apparaître 2 fois.
Région C, 3 ponts, la lettre doit apparaître 2 fois.
Région D, 3 ponts, la lettre doit apparaître 2 fois.
Donc, le parcours doit avoir un minimum de 9 lettres. Or, au point 4, nous avons démontré que la solution du problème exige un parcours de 8 lettres. Donc, la solution cherchée est impossible !!!
Mes constats :
L'énoncé du problème est très simple. À la volée, n'importe qui peut tenter de trouver une route remplissant les conditions. Après quelques essais, on se rend compte qu'y trouver une réponse, par contre, est un défi de taille.
Le problème en soi n'est pas très pratique et ne sert réellement à rien. C'est plutôt une question ludique.
La solution, quant à elle, est brillante. Euler fait d'abord un diagramme de la situation en y accolant quelques symboles. Puis, il formule le problème à partir de raisonnements sur ces symboles. Il constate alors que si la condition du problème est remplie alors elle implique une contradiction. Ce qui signifie que les conditions ne peuvent se réaliser! C'est ce qu'on appelle couramment une preuve par l'absurde : on suppose le problème résolu, et on constate une conséquence impossible !
Aussi, la technique pour le résoudre ressemble étrangement à la méthode du problème de mon billet
La beauté I. Dans ce dernier, on ajoutait de la couleur aux cases et on raisonnait à partir de cette nouvelle dimension. Apposer de la couleur aux cases du damier est équivalent à nommer les régions A, B.. Colorer les dominos est un peu comme noter les ponts a, b, c... Dans les deux cas, les superpositions des réalités (dominos sur cases, ponts sur régions) amènent une impossibilité.
Comme mentionné au billet
La beauté I, il est dans mes convictions profondes qu'il faut baigner l'élève dans ce type de problèmes et dans les solutions apportées. On guide alors l'élève vers des rapprochements heuristiques et méthodologiques.
«L'heuristique se distingue de la méthodologie en ce sens qu'elle est plus une réflexion sur l'activité intellectuelle du chercheur que sur les voies objectives de solution.» (Alain BIROU, 1966)
Dernière remarque : on s'entend généralement pour dire que ce Mémoire est un texte fondateur de ce qu'on connaît aujourd'hui comme la
théorie des graphes.
Lectures suggérées
É. Lucas,
Récréations mathématiques T.1, Albert Blanchard, 1977
Biggs, Lloyd et Wilson,
Graph Theory 1736-1936, Clarendon Press, 1977.
Article Euler, sur
Wikipédia.
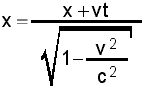 Pour mes billets plus mathématiques, j'ai besoin d'écrire des formules souvent complexes à rendre à l'aide du HTML pur. Et comme le MathML ne semble pas reconnu encore par plusieurs navigateurs, je me suis souvenu d'un script qui m'avait ébloui dans les années 2000. Via Phpinfo, puis Google (car l'hyperlien sur Phpinfo était obsolète), j'ai pu le retrouver. Il est ici. De plus, les sources étant GPL, vous pouvez l'intégrer librement à tous vos scripts !
Pour mes billets plus mathématiques, j'ai besoin d'écrire des formules souvent complexes à rendre à l'aide du HTML pur. Et comme le MathML ne semble pas reconnu encore par plusieurs navigateurs, je me suis souvenu d'un script qui m'avait ébloui dans les années 2000. Via Phpinfo, puis Google (car l'hyperlien sur Phpinfo était obsolète), j'ai pu le retrouver. Il est ici. De plus, les sources étant GPL, vous pouvez l'intégrer librement à tous vos scripts !

 Apnée de Jean-Marie Gourio fait partie de cette catégorie de livres dont je ne sais trop qu'en penser. En résumé, c'est l'histoire d'une femme, Chantal, dont la petite fille de 6 ans se fait violer et tuer par son voisin. Vingt-quatre ans plus tard, elle attend le meurtrier à la sortie de prison : « je ne veux pas me venger, je veux que cet homme me rende mon enfant, elle est à moi, il me l'a prise, il doit me la rendre... » Tout le livre est un voyage dans la tête de cette femme. Évidemment, on peut facilement condamner l'espèce de morbidité maladive de Chantal. Cependant, je crois que s'il m'arrivait de perdre une de mes enfants ou mon petit-fils, il me semble que j'aurais de la misère à m'en remettre « normalement ». Le livre décrit donc une possible survie à cette horreur.
Apnée de Jean-Marie Gourio fait partie de cette catégorie de livres dont je ne sais trop qu'en penser. En résumé, c'est l'histoire d'une femme, Chantal, dont la petite fille de 6 ans se fait violer et tuer par son voisin. Vingt-quatre ans plus tard, elle attend le meurtrier à la sortie de prison : « je ne veux pas me venger, je veux que cet homme me rende mon enfant, elle est à moi, il me l'a prise, il doit me la rendre... » Tout le livre est un voyage dans la tête de cette femme. Évidemment, on peut facilement condamner l'espèce de morbidité maladive de Chantal. Cependant, je crois que s'il m'arrivait de perdre une de mes enfants ou mon petit-fils, il me semble que j'aurais de la misère à m'en remettre « normalement ». Le livre décrit donc une possible survie à cette horreur.

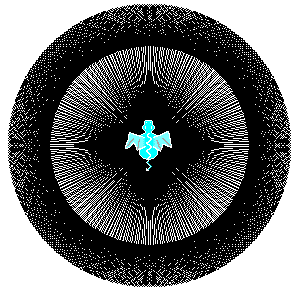 Voici mes deux premières procédures et l'illustration du résultat.
Voici mes deux premières procédures et l'illustration du résultat.
