Comment donner l’illusion d’une accélération est une demande souvent formulée par nos élèves.
Après avoir créé une variable ici appelée « vitesse », le script ci-dessous, trouvé
sur ce wiki, fait le travail.
Dans ce billet, je veux montrer toute la force de Scratch par rapport à l’apprentissage des mathématiques.
Analysons rapidement le script :
- Le drapeau vert lance le script.
- On entame alors une boucle infinie.
- Dans cette boucle, on commence par vérifier si on enfonce la touche FLÈCHE DROITE du clavier. Si c’est le cas, on ajoute 1 à la vitesse.
- On vérifie ensuite si on enfonce la touche FLÈCHE GAUCHE. Et si c’est le cas, on soustrait 1 à la vitesse.
- Ensuite, on multiplie cette vitesse par 0,9.
- Puis on fait avancer la voiture sur l’abscisse selon cette vitesse.
- Et on retourne au début de la boucle.
L’algorithme ne contient aucun objet mathématique très complexe : simple addition (ou soustraction) par 1, et une petite multiplication par 0,9.
Ce n’est pas parce qu’on sait faire des opérations simples sur les nombres qu’on peut anticiper l’effet de ses opérations sur des objets de la vie courante.
Allez-y, et enfoncez la touche flèche droite (ou flèche gauche). Observez la voiture. Essayez de comprendre
pourquoi le script fonctionne.
Le script
communique des instructions à la voiture en utilisant des concepts mathématiques vraiment basiques (addition, multiplication). Et, assez curieusement, on est
surpris que cela fonctionne. Cet étonnement est une bougie d’allumage à l’apprentissage.
Je vous communique ici mon propre processus, celui que j’ai pris pour
m’expliquer le fonctionnement du script.
D’abord, j’ai remarqué que la voiture atteignait une vitesse maximale qu’elle n’arrivait pas à dépasser, peu importe le temps que je tenais enfoncée la touche flèche droite. Le maximum était toujours 9.
Comment donc se faisait-il que je ne puisse dépasser 9 alors que dans la boucle, au moment où j’enfonçais flèche droite, le script
ajoutait toujours 1 ? Ne devais-je pas m’attendre à ce que la vitesse augmente jusqu’à l’infini ?
Je me suis alors mis à jouer le rôle du script.
Voici comment il faut faire.
(On suppose qu’au lancement du script, on tient la touche flèche droite toujours enfoncée.)
| Quand | Vitesse après la touche FD | Vitesse à la fin de la boucle |
| Boucle 1 | 1 | 1 x 0,9 = 0,9 |
| Boucle 2 | 1 + 0,9 = 1,9 | 1,9 x 0,9 = 1,71 |
| boucle 3 | 1+ 1,71 = 2,71 | 2,71 x 0,9 = 2,439 |
| boucle 4 | 1 + 2,439 = 3,439 | 3,439 x 0,9 = 3,0951 |
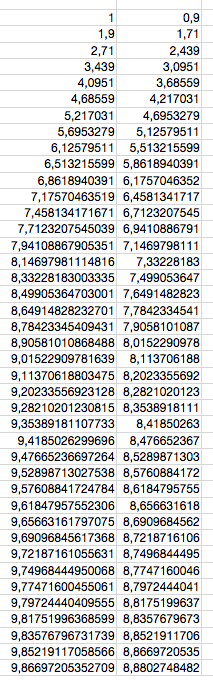
Tout cela, à la main, est un peu fastidieux. Et ce qui m’intéressait était de savoir après 10, 100 ou 1000 accès à la boucle, la vitesse qui en résulterait. Je décidai donc d’ouvrir un tableur pour qu’il fasse les calculs à ma place.
Intéressant n’est-ce pas ? Après une quarantaine d’itérations (passages dans la boucle), on semblait atteindre une limite supérieure égale à 9. En mathématique, on dit que la suite
converge vers 9.
Puis, je me suis mis à la recherche d'une
régularité : je voulais trouver une
formule.
k
0 = 0;
k
1 = 0,9(1+k
0) = 0,9
k
2 = 0,9(1 + k
1) = 0,9 + (0,9)(0,9) = 0,9 + 0,9
2
k
3 = 0,9(1 +k
2) = 0,9 + 0,9(0,9 + 0,9
2) = 0,9 + 0,9
2+ 0,9
3
k
4 = 0,9(1 +k
3) = 0,9 + 0,9(0,9 + 0,9
2 + 0,9
3) = 0,9 + 0,9
2+ 0,9
3 + 0,9
4
et on voit assez clairement (?!) un modèle émerger :
k
n = 0,9
1 + 0,9
2+ 0,9
3 + 0,9
4 + ... + 0,9
n-1 + 0,9
n
Remarque : Je sais que si vos mathématiques scolaires sont un peu loin, toute cette écriture doit vous paraître du chinois. N'y prenez garde pour l'instant, et je vous encourage à lire la suite.
Les mathématiciens ont inventé une notation pour ce genre de «série» :
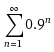
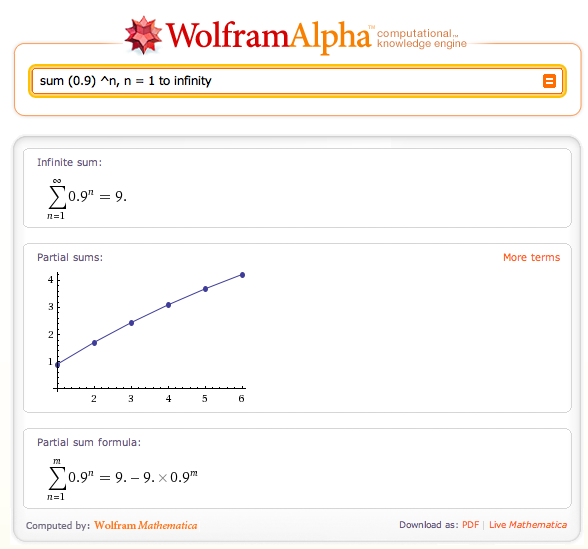
J’ai alors décidé de vérifier à l’aide de
Wolfram|Alpha si la série convergeait « vraiment. »
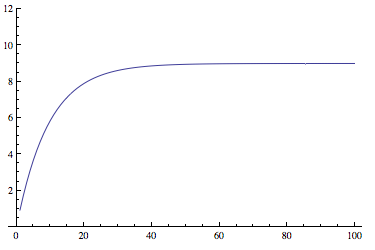
Le graphique ci-contre est aussi très parlant. Dans les premières boucles, la vitesse varie assez rapidement. Puis elle se stabilise.
Un simple script peut nous amener vraiment loin, n’est-ce pas ?
Est-ce à dire qu’il ne faut pas initier les enfants à Scratch parce que les explications sont trop difficiles ? Je dis que c’est tout le contraire. Qu’il faut amener les enfants à réaliser que les mathématiques sont des outils puissants pour, entre autres, modéliser une réalité. L'élève prendra conscience que cette réalité
est modélisable à l'aide d'outils intellectuels profonds. « L'univers est écrit en langage mathématique », disait Galilée.
Alors, que faire avec un enfant de 8 ans qui désire un script de vitesse ? Ne pas lui donner ? Lui dire qu’il va apprendre ça au Cégep ? Lui dire que les mathématiques sont trop compliquées pour lui et qu’il devrait penser à un projet plus «
simple » ?
Je suggère l’approche suivante :
Au primaire : 8-9 ans : Leur remettre le script. On peut demander aux élèves de le modifier pour qu’il réponde à leurs besoins. (Ex. en modifiant le paramètre 0,9)
10-11 ans : Leur remettre le script. Demander aux élèves d’expliquer, en jouant le rôle du lutin, comment les différentes vitesses se calculent. Voyez le premier tableau au début du billet on pourrait demander à l'élève d'en remplir un. J’en profiterais aussi pour ouvrir le chiffrier électronique et leur montrer comment on y fait des calculs répétitifs. Par ailleurs, ce script possède une instruction (avant-dernièere ligne) vraiment intéressante : vitesse = 0.9 x vitesse. Posez la question suivante : Comment se fait-il qu'en ne touchant absolument rien au clavier, la voiture ralentisse et finisse par s'immobiliser ? Cette ligne contient le secret. Demandez aux élèves de vous le révéler.
[Le calcul à la main est beaucoup plus simple. Un chiffrier peut encore être utile ici.]
Au secondaire,
sky is the limit. On envoie les élèves en recherche avec la question suivante : Expliquez-moi
pourquoi le script fonctionne et pourquoi la vitesse ne dépasse pas 9. De là, on ouvre vers l’algèbre, la notation exponentielle, les polynômes, etc. Pour les moins frileux, on peut même avancer des notions du calcul infinitésimal.
J’ai bien peur que ce billet risque d’en décourager plus d’un. Si vous vous dites intérieurement : «
Les élèves ne seront jamais capables », alors Scratch n'est pas pour vous. En effet, on conçoit généralement les notions mathématiques comme un immense escalier qu’on doit absolument grimper en commençant par la première marche. Scratch n’entre pas dans cette vision des choses. Un script devient un objet résultant d’une «
computabilité. » On peut par la suite, tenter de développer le langage qui nous permet d’expliquer l'observation du script en action. Voilà l’espace des mathématiques. C’est ce langage qui tente d’expliquer des phénomènes généralement
computables. Notez aussi qu'une telle exploration d'un script peut nous lancer dans l'adoption d'une notation plus concise. Par exemple, plus haut, j’ai immédiatement utilisé la notation exponentielle. Mais l’élève qui joue le «
computeur » humain recherchant une régularité aboutirait probablement au besoin de cette notation. Par exemple, pour k
4 = 0,9 + 0,9 x 0,9 + 0,9 x 0,9 x 0,9 + 0,9 x 0,9 x 0,9 x 0,9
De la difficulté
Je ne dis pas que l’élève trouvera
facilement les subtilités sous-jacentes à ce script. Après tout, l’enseignant n’est-il pas là pour, justement, amener l’élève à se poser de bonnes questions et à tenter d’y répondre. Je dis bien «
tenter». Il est presque évident que la grande majorité de ses tentatives échoueront. Car, voyez-vous, conceptualiser des éléments computables ne fait pas partie des choses innées de la vie. L’enseignant doit alors
absolument utiliser toute sa puissance émotico-pédagogique pour bien faire «
sentir» à l’élève que c’est bien «
normal» qu’il ne «
sache» pas. Il doit lui faire comprendre que ce qui compte, c’est qu’il essaie
sincèrement de trouver une explication, aussi mince, aussi fragile soit-elle.
Il ne faut pas oublier qu’un élève en apprentissage n’est pas un élève qui sait, mais un élève qui aspire à savoir. Ainsi, peut-être, aura-t-on des élèves heureux d’apprendre que certains mathématiciens ont inventé une écriture (la notation exponentielle) pour des multiplications répétitives.
L’ouverture
Scratch est un logiciel
terriblement ouvert. J’appuie sur le terriblement, car pour y inviter les élèves, un enseignant doit faire preuve d’une grande modestie. C’est un espace où il n’a pas toutes les réponses. Il devra se fier non plus à sa connaissance du problème (et de sa solution) mais plutôt à sa capacité pédagogique d’amener les élèves dans le processus de résolution d’un problème inconnu, problème généralement issu de l’élève même.
La compétence Communiquer à l’aide du langage mathématique.
Le « problème » ci-haut (explication d’un script) relève, à mon avis, de la troisième compétence en mathématique du programme du ministère de l’éducation du Québec. Ce dernier voit l’application de cette compétence ainsi [ceci n'est qu'un exemple, mais ô combien représentatif !] : imaginez une situation complexe (bidon, évidemment) dans laquelle l’élève doit présenter à un conseil municipal la meilleure manière d’aménager un parc public. Puisque l’élève doit
présenter et justifier le résultat de ses calculs, le MELS suggère que l’enseignant évalue cette situation comme faisant partie de la compétence communiquer. C’est, à mon avis, assez simpliste. Pour moi, une compétence s’évalue dans les processus mis en place pour l’activer. Et non par le verbe utilisé dans la question.
Dans le cas de l’activité Scratch ci-haut, l’élève doit décortiquer un script. Cette décortication implique des processus qui peuvent s’activer lors de la lecture du script. On peut donc y observer un élève qui se fait communiquer une information logico-mathématique. Par la suite, un élève qui modifierait la valeur du 0.9 et qui observerait les différentes conséquences, et qui pourrait en faire un bilan mathématique, à mon sens, développe sa compétence en communication mathématique.
Bref, aussitôt qu’un élève
voit et tente de comprendre un
script tiers, nécessairement la compétence communication est activée.
Le potentiel
En conclusion, ce billet voulait démontrer tout le potentiel pédagogique de Scratch. Scratch permet de « computer » facilement, et offre ainsi des possibilités de comprendre ce qui se passe dans un script. C’est de ces possibilités qu’on en tire des bénéfices pédagogiques importants.
 Tout le monde demande une méthode pour bien étudier. Quelque méthode qu'on suive, elle sera inutile, si l’on s'en sert pour apprendre vite. Il n'y a, pour devenir savant, qu'une méthode assurée, c'est d'étudier lentement et avec ordre.
Tout le monde demande une méthode pour bien étudier. Quelque méthode qu'on suive, elle sera inutile, si l’on s'en sert pour apprendre vite. Il n'y a, pour devenir savant, qu'une méthode assurée, c'est d'étudier lentement et avec ordre.



 Tout cela, à la main, est un peu fastidieux. Et ce qui m’intéressait était de savoir après 10, 100 ou 1000 accès à la boucle, la vitesse qui en résulterait. Je décidai donc d’ouvrir un tableur pour qu’il fasse les calculs à ma place.
Tout cela, à la main, est un peu fastidieux. Et ce qui m’intéressait était de savoir après 10, 100 ou 1000 accès à la boucle, la vitesse qui en résulterait. Je décidai donc d’ouvrir un tableur pour qu’il fasse les calculs à ma place.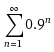

 Le graphique ci-contre est aussi très parlant. Dans les premières boucles, la vitesse varie assez rapidement. Puis elle se stabilise.
Le graphique ci-contre est aussi très parlant. Dans les premières boucles, la vitesse varie assez rapidement. Puis elle se stabilise.

