Exercice préparatoire.
1 - Ouvrez un nouveau projet Scratch.
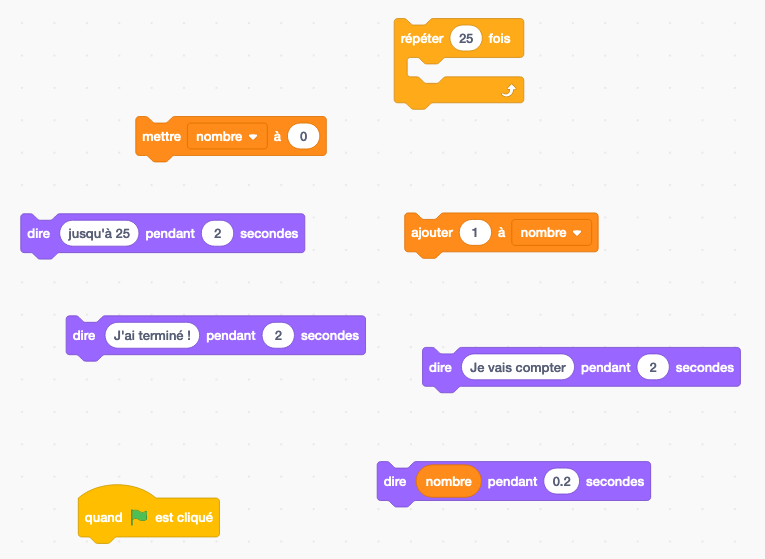
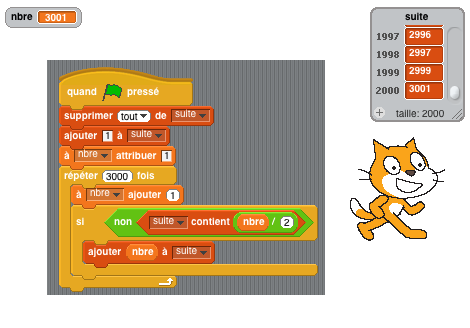
2 - Reproduisez le script suivant et exécutez-le.
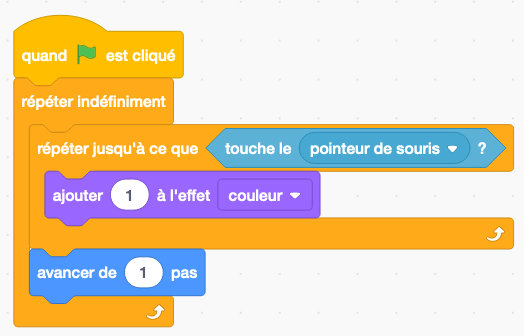
Il est impératif que vous compreniez son fonctionnement (vive la logique!) pour la suite.
Saurez-vous reconstituer ce petit jeu classique :
Cliquez
ICI pour assembler les scripts.
REMIXER
d'ENREGISTRER sous un nouveau nom
et de PARTAGER !
Il est
FORTEMENT suggéré que vous lisiez attentivement tous les scripts avant d'entamer le travail. En les lisant, posez-vous la question « À quoi peuvent-ils servir ? » et tentez d'anticiper calmement leurs potentiels.
À NOTER : Vous ne devez changer AUCUNE VALEUR à l'intérieur des blocs. Il suffit de déplacer les scripts pour les combiner adéquatement. Pour vous faciliter la tâche, certains scripts sont déjà composés de quelques blocs.
Lorsqu'on débogue, il est très utile de VOIR les variables sur la scène. Il suffit de les cocher !
 REMARQUES IMPORTANTES
REMARQUES IMPORTANTES
1- Ce programme comporte une scène et le lutin Devin. Devin a combien de costumes ? Remarquez que chaque costume a un nom bien à lui !
2- Il n'y a qu'une seule brique DRAPEAU VERT et elle se trouve sur la scène. Cependant, une brique ENVOYEZ À TOUS s'y trouve. Il y a donc une brique LORSQUE JE REÇOIS à quelque part... !
3- La brique
DEMANDER --- ET ATTENDRE attend que l'utilisateur entre un nombre. Ce nombre est contenu dans la brique
RÉPONSE.
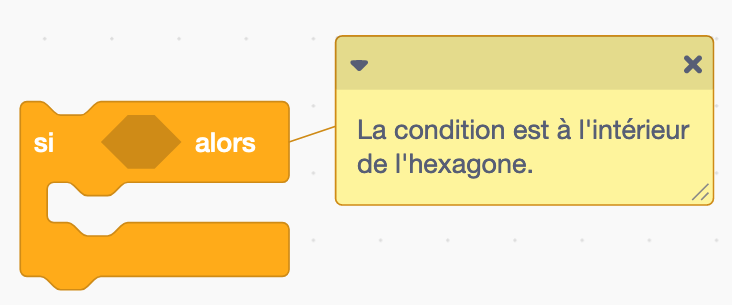
4- Voyez-vous la très grande force de la brique SI --- ALORS ?
5- La brique RÉPÉTER JUSQU'À --- est importante. Le schéma ci-dessous vous aidera à comprendre son fonctionnement.

Défis
A - Modifiez le jeu pour que le nombre secret soit entre 1 et 50
B - Créez un deuxième personnage qui affichera sa réponse. N'oubliez pas que lorsqu'on désire que deux lutins communiquent, il est généralement nécessaire d'inclure une combinaison du genre :
Envoyer à tous et
Quand je reçois. Cela pourrait donner quelque chose comme :
Un peu de mathématique
A) Auriez-vous pu modifier les deux conditions dans les briques SI --- ALORS pour avoir un résultat identique ? HINT : 8>4 n'est-il pas identique à 4<8?
B) Il a été découvert qu'un bon joueur trouvera TOUJOURS le nombre secret en 7 tentatives ou moins. Expliquez pourquoi.
C) Dans le même ordre d'idée que la question (B), combien de tentatives
au maximum pourrait-il être nécessaire à un
bon joueur pour trouver un nombre secret entre 1 et 200 ? Entre 1 et 1000 ? Testez votre réponse à l'aide de votre programme.
NOTES PÉDAGOGIQUES
1 - Les élèves DOIVENT ABSOLUMENT lire tous les scripts avant d'entamer quoi que ce soit.
2 - Réviser si nécessaire les concepts de
nombre aléatoire, de
plus grand et
plus petit.
3 - Le bloc RÉPÉTER JUSQU'À -- a une logique bien particulière. S'assurer que les élèves le maîtrisent.
4 - Il faut remarquer les stratégies qu'auront les élèves pour trouver le nombre secret.
5 - Pour résoudre ce problème, la division est une opération qui sera sans doute utilisée par les élèves.
6 - On peut faire réfléchir les élèves avec une question du genre : «Si de 0 à 100, on peut trouver en 7 tentatives, cela prendra-t-il au maximum 14 tentatives à un bon joueur pour trouver le nombre secret entre 1 et 200? »
7 -
SI ET SEULEMENT SI LES ÉLÈVES TROUVENT LA MANIÈRE OPTIMALE de résoudre le jeu, on pourra les initier au concept de puissance : Ex. 2
7 = 2x2x2x2x2x2x2=128
8 - Pour aller un peu plus loin, on pourra discuter avec les élèves du
paradoxe de Zénon en leur racontant l'histoire d'Achille et la tortue.