Utility as a goal is inferior to elegance and profundity.
Davis et Hersh, The mathematical experience.
Quand je pense aux mathématiques et à ce qu'elles m'ont apporté, c'est cette qui preuve me vient à l'esprit. J'étais sur les bancs de l'Université et aussitôt la démonstration terminée par le professeur, je suis resté sous le choc de l'émerveillement. Je me comptais chanceux d'être en vie et pouvoir goûter à une telle beauté. Plusieurs années plus tard, j'ai voulu transmettre mon enthousiasme, et j'ai pondu cette
dialoguerie. Je sais bien qu'on ne peut pas tous aimer les
Préludes et Fugues de Bach, ou la peinture de Miro ou les romans de Kundera, mais si par ce texte j'arrive à témoigner juste un petit peu de la fascination des mathématiques, alors j'aurais atteint mon but. (Oct. 2006)
Cet article est paru dans la revue ENVOL du mois de novembre 1995
La question
Élève (assis confortablement près
du professeur): Il est écrit ici, dit-il en montrant son
livre, que 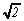 est i-r-r-ationnel. Ça
veut dire quoi ce mot-là?
est i-r-r-ationnel. Ça
veut dire quoi ce mot-là?
Le professeur s'apprêtait à répondre mais
l'élève reprit aussitôt:
Élève: Je suppose que ça signifie qu'il n'est
pas rationnel. Mais qu'est-ce que ça change qu'il soit
rationnel ou non???
Professeur: Connais-tu Hippasus?
E (moqueur): C'est un nouvel enseignant de l'école ?
P : Mais non! Hippasus, c'est le type qui a découvert que
cette racine carrée n'était pas rationnelle. Cela
fit une terrible histoire. Vers le 5è siècle avant
Jésus-Christ, Pythagore avait fondé une espèce
de confrérie plus ou moins secrète dont le credo
était que l'univers peut être connu par des nombres
entiers ou des rapports de nombres entiers. Hippasus, par sa découverte,
jetait le discrédit sur cette école de pensée.
C'était grave... tellement grave que les pythagoriciens
ont jeté le pauvre Hippasus au beau milieu de la Méditerranée
pour ne pas qu'il ébruite la nouvelle. Il est mort noyé.
Élève (incrédule): Aie! C'était dangereux
de faire des maths à cette époque...
P (changeant le sujet): Tu as appris que si un nombre décimal
a dans son développement une répétition à
l'infini, alors ce nombre est exprimable sous la forme de fraction,
c'est-à-dire de nombre rationnel.
L'élève cherchait dans sa mémoire. Mais,
à l'évidence, cette dernière lui faisait
fausse route. Cependant, après un bref rappel de la part
du professeur, tout se remit en ordre dans le cerveau de l'élève.
P : Prenons la calculatrice et demandons-lui de calculer cette
fameuse racine de deux.
L'élève s'empressa d'ordonner à la petite
machine de lui livrer le résultat de ce calcul. Il trouva
alors à l'écran d'affichage la valeur 1,414213562.
E (tout content): Oh, je comprends! Dans ces décimales,
il n'y a pas de répétition à l'infini, donc
il n'est pas rationnel.
L'élève s'apprêtait à quitter sa place
lorsque le professeur le retint.
P : Attends! Comment peux-tu être bien certain que, vers
les milliards de milliards de décimales, on ne finisse
pas par trouver un développement périodique? Après
tout, la calculatrice ne te donne que ce qu'elle peut afficher
dans son écran. Tu n'as aucune indication sur ce qui arrive
au-delà de cet affichage.
E : Mouain...
P (satisfait d'avoir semé le doute chez l'élève):
Et bien moi, je vais te prouver, oui, oui, te P-R-O-U-V-E-R, qu'il
n'y a pas de tel développement périodique pour la
racine carrée de deux.
E (inquiet): Est-ce que c'est facile à comprendre?
P (haussant les épaules): Facile? Je ne sais pas. Mais
la preuve est de toute beauté et elle mérite bien
le peu d'efforts que tu auras à mettre à la comprendre!
Je vais donc te prouver qu'il est impossible de mettre sous forme
fractionnaire le nombre 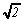
Une nouvelle définition
P: (relevant ses manches): Je dois d'abord te montrer une nouvelle
définition. Tu verras, elle est bien simple à comprendre
et c'est grâce à elle que je pourrai te faire la
démonstration. Je vais définir ce que j'entends
par fraction irréductible.
E (reculant sur son siège): Yack, je sens que ça
va être compliqué...
P : Mais non! Tu sais que certaines fractions sont simplifiables.
Par exemple, le nombre 4/12 devient 1/3 lorsqu'on réduit
par 4. Un autre exemple serait 10/100 qui devient 1/10 si on...
E : Réduit par 10. C'est élémentaire tout
ça.
P (souriant): Oui. Je dirai donc d'une fraction qu'elle est IRREDUCTIBLE
si elle a été simplifiée au maximum. Par
exemple, 15/25 n'est pas irréductible car on peut simplifier
par 5. Cependant 3/5 est une fraction irréductible. Tu
vois?
E (bien rassuré qu'un mot si long désigne un phénomène
si simple): Oui, je comprends bien ça!
Le professeur sentait bien que son élève avait saisi
cette idée. Il savait tout aussi bien qu'il n'en comprendrait
toute la portée qu'à la fin de la preuve.
L'algèbre est de paire
P : Peux-tu me dire ce qu'est un nombre pair?
E : Je ne vois pas le rapport avec...
Le professeur lui coupa la parole.
P : Tut, tut, tut. Tu verras le rapport plus tard. Il est essentiel
que tu saches ce qu'est un nombre pair. Sinon tu n'y comprendras
rien à la preuve et...
E (haussant à son tour les épaules): Un nombre pair
est un nombre qui est divisible par deux. Et j'ajoute qu'un nombre
impair en est un qui ne se divise pas par deux. Tout le monde
sait ça!
Le professeur sortit de son tiroir quelques feuilles vierges. En
prenant une, il demanda à l'élève de lui
écrire, en colonne, quelques nombres pairs. L'élève
y inscrivit les nombres suivants:
2
4
6
Puis, lorsque le professeur lui demanda d'en écrire de
plus gros, il ajouta:
100
104
200
P : Parfait. Maintenant observe bien ce que je fais faire.
Le professeur inscrivit sur la feuille une deuxième colonne.
La page ressemblait à celle-ci:
| 2 | 2 x 1
|
| 4 | 2 x 2
|
| 6 | 2 x 3
|
| 100 | 2 x 50
|
| 104 | 2 x 52
|
| 200 | 2 x 100
|
Tout en écrivant cette nouvelle colonne, le professeur
expliquait.
P : Tu vois? Tout nombre pair peut s'exprimer sous cette forme:
2 fois quelque chose.
Puis il ajouta sur la feuille:
| ... | ...
|
| 100 | 2 x 50
|
| 104 | 2 x 52
|
| 200 | 2 x 100
|
un nombre pair quelconque = 2 fois quelque chose.
P (regardant et pointant du crayon cette dernière phrase):
Je vais maintenant utiliser l'écriture algébrique.
Sous la dernière ligne, il ajouta:
un nombre pair quelconque = 2 fois n
ou 2n.
P : Le "n" représente tout simplement un entier
quelconque. Il est plus simple d'écrire 2n que d'écrire
"deux fois quelque chose"...
E : Oui, je comprends.
P (voulant résumer): On peut donc écrire tout nombre
pair sous la forme 2n où n est un entier quelconque.
Le professeur jeta alors un oeil vers son élève
et lui demanda:
P : Comment écrirais-tu un nombre impair dans cette écriture
algébrique?
E (au bord de la panique): ???
Le professeur refit alors la même démarche que précédemment.
Il demanda à l'élève d'inscrire des impairs
sur une feuille blanche. Puis il ajouta une deuxième colonne.
Voilà à quoi ressemblait cette page.
| Choix de l'élève | Le professeur ajouta
|
| 3 | 2 x 1 + 1 |
| 5 | 2 x 2 + 1 |
| 7 | 2 x 3 + 1 |
| 101 | 2 x 50 + 1 |
| 143 | 2 x 71 + 1 |
P : Alors? Vois-tu comment écrire sous forme algébrique
tout nombre impair?
E (hésitant): Hum... On peut dire qu'un nombre impair est
toujours égal à deux fois quelque chose plus 1.
Donc si je remplace la mot quelque chose par la lettre
n, on a:
Un nombre impair quelconque = 2n + 1.
P : Bravo! Tu as bien compris. Pendant que nous y sommes, nous
allons prouver que le carré de tout nombre impair est
lui-même impair.
Impair carré est impair
E : Mais je croyais que nous devions démontrer que la racine...
P : Oui, je sais. Mais tu verras, cette preuve est intéressante!
Et puis le fait que tout carré d'un nombre impair soit
lui-même impair fait partie intégrante de la preuve
recherchée.
L'élève fronça alors les sourcils car il
ne savait absolument pas où allait le professeur. Cependant,
il voyait bien que ce dernier s'amusait grandement à tenter
de lui faire cette preuve. Et, pour le moment, voir le professeur
"tripper" ainsi était bien suffisant pour
tenter de le suivre.
P (remarquant que son pupille rêvassait) Alors tu me suis
ou quoi?
E (souriant): Oui, oui.
Ce fut au tour du professeur de regarder intensivement son élève.
Il se demanda un court instant s'il valait vraiment la peine de
prendre tout ce temps pour lui expliquer une si belle preuve.
Après tout, il savait fort bien que d'ici quelques heures,
l'élève aurait tout oublié. Mais cette preuve
est si jolie...
P (revenant sur terre): Bon. Regarde bien ces nombres
5
11
33
57
101
Tu es certainement d'accord pour dire que ce sont tous des nombres
impairs. Inscris au côté de ces nombres leur carré.
Tu peux utiliser la calculatrice.
L'élève s'appliqua à exécuter cette
simple consigne. Le résultat fut le suivant:
5 25
11 121
33 1089
57 3249
101 10201
P : Que remarques-tu à propos de ces carrés?
E : ???
P : Quelle sorte de nombres a-t-on?
E : Bien, des naturels!
P (un peu exaspéré): Oui, je sais bien que ce sont
des naturels, mais ne remarques-tu pas que tous ces carrés
sont IMPAIRS?
E : Oui, bien sûr!
P : Voilà ce que je veux te démontrer: que le carré
d'un nombre impair est TOUJOURS impair.
E : Ça m'a l'air évident.
P (haussant légèrement le ton): Comment cela, ÉVIDENT???
E : Je vois bien qu'avec les nombres inscrits que...
P (coupant court aux explications de l'élève): Mais
ne crois-tu pas possible que dans les milliards de milliards,
par exemple, il puisse se trouver un impair dont le carré
ne soit pas impair?
E : Je ne sais pas pourquoi, mais il me semble que même
dans les milliards de milliards, le carré de ce nombre
serait impair.
P : Tu as une bonne intuition. Mais il faut maintenant justifier
cette intuition par une PREUVE. Nous allons utiliser le pouvoir
de l'algèbre pour démontrer que le carré
de tout nombre impair est impair.
Puis le professeur continua.
P : Prenons un nombre impair quelconque.
Le professeur fit alors sentir à l'élève
qu'il devait écrire quelque chose sur la feuille.
E: ???
Le professeur, voyant que l'élève ne savait que
faire, inscrivit: 2n + 1.
P : Es-tu d'accord pour dire que ce 2n + 1 représente un
nombre impair quelconque?
L'élève, déçu de ne pas avoir pensé
à cette formule acquiesça.
P : Peux-tu maintenant calculer le carré de ce nombre?
E : ???
P : Que vaut le carré de 2n + 1?
L'élève hésitant grandement se risqua tout
de même à une réponse:
E : 4n2 + 1, dit-il faiblement comme pour étouffer
un mauvais sort.
P (encourageant): Ce n'est pas la réponse exacte mais c'est
tout de même un bel essai. Rappelle-toi la définition
du carré d'un nombre: le carré d'un nombre est
le produit de ce nombre par lui-même. Il faut donc multiplier
ce nombre impair quelconque par lui-même.
L'élève inscrivit alors sur la feuille:
2n + 1
x
2n + 1
P : Oui, c'est bien cela. Et quel est le résultat de cette
opération?
En se rappelant alors la manière de multiplier des binômes,
l'élève inscrivit:
2n + 1
X
2n + 1
4n2 + 2n
2n + 1
4n2 + 4n + 1
P : Bravo! Que peut-on dire à propos de ce résultat?
E : ???
P : Regarde bien le résultat: 4n2 + 4n + 1.
Es-tu d'accord pour dire que le terme 4n2 est pair
car il est divisible par deux? (L'élève acquiesça).
Puis pour dire que le terme 4n est aussi un nombre pair car il
est divisible par deux? On a donc:
4n2 + 4n + 1
(un pair) + (un pair) + 1
Tu me suis?
E : Oui.
P (sceptique): Bon. Vois-tu qu'en additionnant deux nombres pairs,
le résultat est nécessairement pair?
E : Comment pourrais-je en être certain. Peut-être
que dans les milliards de...
P : Penses-y un peu. La somme de deux nombres divisibles par deux
est nécessairement divisible par deux. C'est un peu comme
si ces deux nombres avaient au moins un diviseur commun
soit 2! Regarde les exemples suivants:
52 + 246 = 2 fois (26 + 143)
466 + 2 = 2 fois (233 + 1)
2k + 2n = 2 fois (k + n).
L'élève assura le professeur qu'il venait de comprendre
que la somme de deux nombres pairs est nécessairement un
nombre pair.
P : Donc on a (un pair) + (un pair) + 1 = (un pair) + 1.
E : Ouain... mais je ne sais même pas quelles valeurs ont
tous ces nombres pairs entre parenthèses.
P : Tu as bien raison mais, comme tu viens de le dire, on ne sait
pas ce que valent ces nombres PAIRS. Mais on sait, tout au moins,
qu'ils sont pairs.
E : Oui, mais moi j'aimerais bien savoir quels sont ces nombres.
P (souriant): Je résume. On a élevé au carré
un nombre impair quelconque et on s'est aperçu que
le résultat donnait quelque chose qui ressemble à
un nombre pair quelconque + 1:
(impair)2 = (pair) + 1.
E (lumineux): Mais oui! Et un nombre pair plus un est nécessairement
un nombre impair même si je ne connais pas sa valeur.
P (toujours souriant et fier de sa propre patience): Voilà!
E (redevenu normal): Et l'algèbre dans tout cela? Je ne
m'en suis servi que pour la multiplication des binômes.
P : Tu es très perspicace. Ce que nous avons fait, c'est
l'intuition et le raisonnement qui nous y a conduit. Mais cette
approche serait tout à fait inacceptable dans un livre
de maths qui se respecte. Regarde bien: je vais te faire cette
même preuve, mais cette fois dans un langage mathématique
correct.
Étape 1: Soit 2n + 1 un nombre impair quelconque.
Étape 2: Alors 4n2 + 4n + 1 est son carré.
Étape 3: Mais 4n2 peut s'écrire sous
forme 2x où x = 2n2 et 4n peut s'écrire
sous forme 2y où y = 2n.
Étape 4: Or 2x + 2y peut s'écrire sous la forme
2k où k = x + y.
Étape 5: D'où (2n+1)2 = 2k+1 ce qui est
bien la forme d'un nombre impair.
E : Wow!
P (regardant sa preuve avec admiration): Remarque bien que toutes
les étapes qu'on a faites sont ici écrites en remplaçant
les mots tels un pair, un impair, etc. par leur forme algébrique.
C'est plus concis et c'est plus clair.
E : Clair mon oeil!
P : Ne t'en fais pas trop: l'algèbre est une science difficile
à maîtriser et tu dois te donner des chances. Garde
seulement en mémoire que, dans le fond, l'algèbre
sert à traduire dans un langage universel les idées
sur les nombres et leurs relations. Mais ça prend de l'expérience
pour la contrôler et aujourd'hui, tu viens d'en gagner un
peu plus.
E : Je ne dois donc pas m'en faire si l'aspect écriture
algébrique n'est pas aussi clair pour moi?
P : C'est cela. D'ailleurs, je pense que tu as très bien
saisi que peu importe le nombre impair que je choisis, son carré
sera toujours impair. L'écriture algébrique est
peut-être encore un peu confuse pour toi, mais au moins,
tu as compris l'idée. L'algèbre n'est qu'une façon
pratique, lorsqu'on la maîtrise, de traduire des
idées.
L'absurde entre en jeu
P : On continue?
E : Je ne sais plus trop où j'en suis rendu!
P : Nous cherchons à démontrer que 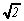 n'est pas un nombre rationnel. J'ai commencé par te donner
la définition d'une fraction irréductible puis je
t'ai prouvé que le carré de tout nombre impair est
aussi un nombre impair. On a maintenant tout en ... tête...
pour répondre à la question de départ. Pour
ce faire je vais procéder par l'absurde.
n'est pas un nombre rationnel. J'ai commencé par te donner
la définition d'une fraction irréductible puis je
t'ai prouvé que le carré de tout nombre impair est
aussi un nombre impair. On a maintenant tout en ... tête...
pour répondre à la question de départ. Pour
ce faire je vais procéder par l'absurde.
E : Par QUOI???
P (en appuyant sur le mot): Par l' A B S U R D E.
E : Et moi qui croyais que les mathématiques étaient
une chose sérieuse.
P (cherchant ses mots): Je vais raisonner par l'absurde. Cela
consiste à tenir pour acquis qu'un certain fait est vrai,
pour ensuite démontrer que le fait que ce fait soit vrai
amène une contradiction et donc de conclure que le fait
en question doit être faux. Simple n'est-ce-pas?
E : HEIN?????????
P (se grattant la tête et soupirant): Ok... oublie ce que
je viens de te dire. Je reviendrai sur ce type de raisonnement
un peu plus tard. Pour le moment, essaie de me suivre. Je vais
partir de l'hypothèse suivante: nous allons supposer que
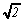 est un nombre rationnel.
est un nombre rationnel.
E : Pourquoi?
P : Bien, pourquoi pas? Es-tu d'accord avec ce qui suit: ou
bien 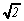 s'écrit sous forme fractionnaire
ou bien
s'écrit sous forme fractionnaire
ou bien 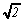 ne s'écrit pas sous forme
fractionnaire?
ne s'écrit pas sous forme
fractionnaire?
E (qui n'était plus très certain de la compétence
de son prof. depuis que ce dernier lui avait parlé d'absurdité):
Je ne vois pas très bien à quoi cela nous avance
de mentionner des évidences pareilles!
P (content de voir que son élève n'avait pas de
problème avec la logique): Tu vas voir très bientôt
l'utilité d'énoncer clairement des évidences.
Donc, je vais supposer que 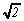 s'écrit
sous forme fractionnaire. Je vais alors te montrer que cette supposition
amène une conséquence tout à fait illogique.
C'est cela faire une preuve par l'absurde!
s'écrit
sous forme fractionnaire. Je vais alors te montrer que cette supposition
amène une conséquence tout à fait illogique.
C'est cela faire une preuve par l'absurde!
E (incrédule): J'ai hâte de voir ça...
Le professeur esquissa un léger sourire puis poursuivit.
P : Donc je suppose que 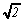 s'écrit
en fraction. Cela veut dire que je peux trouver deux nombres entiers,
appelons-les "a" et "b" par exemple, tels
que
s'écrit
en fraction. Cela veut dire que je peux trouver deux nombres entiers,
appelons-les "a" et "b" par exemple, tels
que 
E : Donc "a sur b" représente la manière
d'écrire sous forme fractionnaire la racine carrée
de deux.
P : C'est cela. Mais on va supposer, si tu es d'accord, que cette
fraction est irréductible, c'est-à-dire qu'elle
a été simplifiée au maximum et...
E : Oui, oui, je suis d'accord.
P : Regarde bien! Puisque 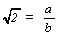 , on peut donc
dire que
, on peut donc
dire que 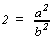 .
.
E: Eeeeeeeeeeeeeeee...
P: J'ai élevé au carré les deux membres de
l'équation.
E (après un semblant de réflexion): Je vois...
P (incrédule...) Je continue. Puisque 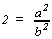 ,
es-tu d'accord avec moi pour dire que 2b2=a2?
,
es-tu d'accord avec moi pour dire que 2b2=a2?
Élève: Mmmm...Oh oui! On a envoyé le b2
de l'autre côté de l'équation. J'ai déjà
appris cela...
Prof (fier de son enseignement) Tu as une très bonne mémoire.
Mais remarques-tu quelque chose de particulier à propos
de cette équation?
É: Bof...
P: Peux-tu trouver une qualité à a2?
E: ?????
P: Puisque a2 est égal à deux
fois b2, ne peut-on pas dire que a2 est...
pair?
E: Mais oui, bien sûr. On a vu cela tantôt.
P (soulagé): Donc si a2 est pair, il faut nécessairement
que a soit aussi pair.
E: Comment cela?
P (content de la question): Mais tout simplement parce que s'il
était impair, son carré aussi le serait. On a vu
cela tantôt! Donc, puisque "a" n'est pas impair,
il est nécessairement pair!!! On peut donc l'écrire
sous la forme de deux fois quelque chose. On a donc:
a = 2 n
où n représente quelque chose...
E: Je ne vois pas tellement à quoi ça nous avance
de faire ce tour de passe-passe.
P (presque choqué): Ce n'est pas un tour de passe-passe.
Mais enfin, es-tu d'accord avec cette dernière équation?
E: Mais oui.
P: L'équation 2b2 = a2 peut donc
maintenant s'écrire 2b2=(2n)2.
E: Pourquoi les parenthèses?
P: Hum.. Ok, on efface.
Et le professeur effaça cette dernière équation
pour y substituer celle-ci: 2b2 = a ´
a.
P: Et maintenant, es-tu d'accord avec cette équation?
E: Mais oui car a2 signifie a fois a.
P (satisfait): Mais on a trouvé que "a" est un
nombre pair et donc qu'il peut s'écrire sous la forme 2n.
L'équation devient donc: 2b2 = 2n ´
2n. Ce qui veut dire: 2b2=4n2
E: Oui, oui, je suis d'accord.
P (fébrilement): Et si on réduit par deux les deux
membres de l'équation, on a: b2=2n2
E: Oui!
P: Bien. Peux-tu maintenant me dire quelque chose de spécial
à propos de b2?
E (Hésitant): Bien...
Le professeur pointe le "2" dans l'équation.
E: Oh oui! il est pair. b2 est pair.
P: Et donc...?
E: Et donc... hum ... "b" est aussi pair car s'il était
impair, b2 serait aussi impair. C'est le même
tour de passe-passe que tantôt.
P (hautement): Donc "a" est pair ET "b"
est pair.
Puis après un bref silence, le professeur ajouta fièrement:
P: Et c'est pour cela que 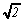 est irrationnel!!!
est irrationnel!!!
E (levant les sourcils): Je ne vois pas le rapport.
P: Et pourtant le rapport est là, devant tes yeux.
E: ????????
P: Mais oui! Si "a" ET "b" sont pairs,
cela veut dire que la fraction que nous avions au début,
soit 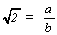 N'EST PAS IRRÉDUCTIBLE
puisqu'on peut la simplifier par deux. Ma supposition de départ,
à savoir qu'il existe une fraction irréductible
qui peut représenter
N'EST PAS IRRÉDUCTIBLE
puisqu'on peut la simplifier par deux. Ma supposition de départ,
à savoir qu'il existe une fraction irréductible
qui peut représenter 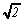 amène
une contradiction. Cela veut dire que cette hypothèse est
fausse. On doit donc conclure qu'il n'existe pas de fraction qui
peut représenter
amène
une contradiction. Cela veut dire que cette hypothèse est
fausse. On doit donc conclure qu'il n'existe pas de fraction qui
peut représenter 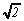 .
.
E: Wow!
Notes pédagogiques (Oct. 2006)
- Avec les maths modernes, la notion de preuve est presque disparue de nos programmes. Je crois cependant qu'en prouvant des théorèmes aux élèves, on peut accrocher certains esprits curieux de la logique interne de la reine des science.
- Dans cette démonstration, l'algèbre (comme le carré d'un binôme) peut sans doute en décourager plus d'un. Cependant, si l'élève n'a pas encore appris cette notion, il est tout de même possible de lui faire goûter cette preuve en procédant par plausibilité : on rend plausible que le carré d'un impair est impair et que le carré d'un pair est pair en faisant sentir à l'élève ce qui se passe.
- Au lieu de commencer par cette preuve, on peut par exemple faire la démonstration de la formule des nombres triangulaires (ou de tout autre nombre figuré), démonter le théorème de Pythagore avec un logiciel de géométrie dynamique, etc. L'idée est surtout d'illustrer la beauté du raisonnement déductif.
 Dernier roman de Perutz, Le Judas de Léonard est une fort agréable lecture. Pour sa peinture de la cène, Léonard de Vinci cherche le bon visage, celui dont les traits répondraient « au péché d'orgueil qui conduisit Judas à trahir l'amour qu'il éprouvait. » Joachim Behaim deviendra son Judas, et c'est son histoire que Perutz raconte. L'une des
Dernier roman de Perutz, Le Judas de Léonard est une fort agréable lecture. Pour sa peinture de la cène, Léonard de Vinci cherche le bon visage, celui dont les traits répondraient « au péché d'orgueil qui conduisit Judas à trahir l'amour qu'il éprouvait. » Joachim Behaim deviendra son Judas, et c'est son histoire que Perutz raconte. L'une des 
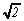 est i-r-r-ationnel. Ça
veut dire quoi ce mot-là?
est i-r-r-ationnel. Ça
veut dire quoi ce mot-là?
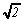
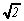 n'est pas un nombre rationnel. J'ai commencé par te donner
la définition d'une fraction irréductible puis je
t'ai prouvé que le carré de tout nombre impair est
aussi un nombre impair. On a maintenant tout en ... tête...
pour répondre à la question de départ. Pour
ce faire je vais procéder par l'absurde.
n'est pas un nombre rationnel. J'ai commencé par te donner
la définition d'une fraction irréductible puis je
t'ai prouvé que le carré de tout nombre impair est
aussi un nombre impair. On a maintenant tout en ... tête...
pour répondre à la question de départ. Pour
ce faire je vais procéder par l'absurde.
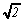 est un nombre rationnel.
est un nombre rationnel.
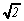 s'écrit sous forme fractionnaire
ou bien
s'écrit sous forme fractionnaire
ou bien 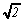 ne s'écrit pas sous forme
fractionnaire?
ne s'écrit pas sous forme
fractionnaire?
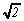 s'écrit
sous forme fractionnaire. Je vais alors te montrer que cette supposition
amène une conséquence tout à fait illogique.
C'est cela faire une preuve par l'absurde!
s'écrit
sous forme fractionnaire. Je vais alors te montrer que cette supposition
amène une conséquence tout à fait illogique.
C'est cela faire une preuve par l'absurde!
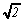 s'écrit
en fraction. Cela veut dire que je peux trouver deux nombres entiers,
appelons-les "a" et "b" par exemple, tels
que
s'écrit
en fraction. Cela veut dire que je peux trouver deux nombres entiers,
appelons-les "a" et "b" par exemple, tels
que 
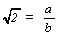 , on peut donc
dire que
, on peut donc
dire que 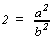 .
.
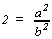 ,
es-tu d'accord avec moi pour dire que 2b2=a2?
,
es-tu d'accord avec moi pour dire que 2b2=a2?
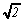 est irrationnel!!!
est irrationnel!!!
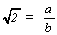 N'EST PAS IRRÉDUCTIBLE
puisqu'on peut la simplifier par deux. Ma supposition de départ,
à savoir qu'il existe une fraction irréductible
qui peut représenter
N'EST PAS IRRÉDUCTIBLE
puisqu'on peut la simplifier par deux. Ma supposition de départ,
à savoir qu'il existe une fraction irréductible
qui peut représenter 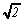 amène
une contradiction. Cela veut dire que cette hypothèse est
fausse. On doit donc conclure qu'il n'existe pas de fraction qui
peut représenter
amène
une contradiction. Cela veut dire que cette hypothèse est
fausse. On doit donc conclure qu'il n'existe pas de fraction qui
peut représenter 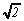 .
.

