Jobineries

« Ce n'est pas la formule gagnante de boycotter le rêve des enfants. »
Jean-Marc Fournier, ministre de l'Éducation, Matinternet : manchette du 25 octobre.

Dire que ce sont mes taxes qui payent le salaire de ce ministre. Son mépris pour le personnel enseignant me donne mal au coeur car ce que je vois chaque jour, ce sont des enseignants et des enseignantes qui travaillent pour que les rêves des enfants, justement, se réalisent.

Albert Brie a signé, au cours des années '70 et '80, une chronique intitulée Le mot du silencieux. Deux compilations rendent compte de cet aphoriste acerbe. Vous ne les trouverez que chez les bouquinistes comme Abebooks. On peut lire en quatrième de couverture du Retour du silencieux (Boréal, 1989) qu'Albert Brie «maîtrise l'art difficile de la formule courte qui fait réfléchir sans assommer, qui fait sourire et même rire tout en visant juste.» Je partage cet avis. On trouve peu d'information sur le web concernant cet auteur québécois né en 1925, mais ici, on apprend qu'il a été l'un des scénaristes des Enquêtes Jobidon, une émission que je suivais assidûment dans ma jeunesse!

J'ai déjà plusieurs citations de M. Brie sur Au fil de mes lectures provenant de vieilles découpures du Devoir. Vous en trouverez plusieurs autres au cours des prochaines semaines car je termine tout juste Le mot du silencieux (Fides, 1978).

En voici d'ailleurs quelques extraits autour du thème de la politique.

Pour défendre sa langue, la parlant français doit être vigilant ; l'Anglais pour faire usage de la sienne n'a qu'à être là où il se trouve.

Quand un discours politique a de l'élévation, de la vigueur, de l'élégance, de la tenue, détrompons-nous ! ce n'en est pas un.

Tous les politiciens sont opportunistes ; les plus habiles le sont au moment opportun.

Il ne mentait pas ce député qui lançait à ses électeurs : « Ma porte est toujours ouverte. » Il se gardait bien d'ajouter qu'il n'était pas dans la pièce.

La plupart des gens qui se passionnent pour les luttes électorales ne portent ordinairement aucun intérêt à la vie politique dans son cours normal. En cela, ils suivent l'exemple de bon nombre de politiciens qui s'agitent avec fureur durant un ou deux mois que dure la campagne électorale. On les trouve abîmés dans un sommeil comateux pour les trois ou quatre ans qui précèdent le prochain match.

Et une citation utile à Mme Marois.
Mon sentiment est qu'il faut voter pour le meilleur homme, surtout si c'est une femme.

En politique, s'expliquer c'est mentir, mais en beaucoup plus de mots.

Récemment, un sondage indiquait qu'une majorité de Québécois pense que les politiciens sont menteurs. Voici ce qu'en disait M. Brie en 1978:
Il est bien admis que les politiciens pratiquent couramment le mensonge. Si l'un d'eux prend l'habitude de dire la vérité, le peuple peut aller jusqu'à se demander si cet original ne manque pas à son devoir professionnel.

P représente l'enseignant et E, l'élève.

Contexte : l'élève doit passer une heure en cours de récupération avec un enseignant car on a détecté qu'il avait un sérieux problème de compréhension de l'addition et de la soustraction chez les entiers.

P : On va commencer par faire un petit résumé de ce que sont les entiers.
E (haussant les épaules): Les nombres entiers ? Bof, ce sont les plus et les moins...
P (sentant qu'il aura du plaisir avec son élève) : Hum... En fait, c'est beaucoup plus simple que ça. Les nombres entiers représentent des quantités qui peuvent avoir un opposé. Par exemple, les couples (gagner, perdre), (avancer,reculer), (monter, descendre), (électron, positron)...
E (coupant l'enseignant) : C'est quoi un positron?
P (content de recevoir cette question) : En quelque sorte, c'est le contraire d'un électron. En fait, si tu colles un électron à un positron il en résultera, grosso modo, une annihilation. C'est comme s'ils disparaissaient. En réalité, il résulte de cet affrontement une espèce d'énergie radiante.
E (hésitant): L'antimatiere ?
P (de plus en plus heureux de travailler avec cet élève) : Exactement! Les nombres entiers sont là pour représenter, en quelque sorte, l'idée d'opposition. Pour bien illustrer la chose, je vais prendre un modèle qui devrait t'aider à comprendre comment tout cela fonctionne.
L'enseignant sortit son jeu de go contenant des pierres blanches et des pierres noires. Puis il lui expliqua :
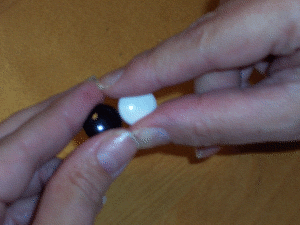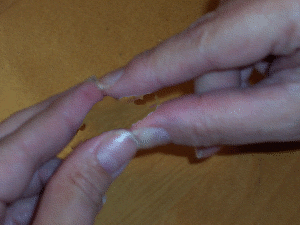
P : Tu vois, on a ici une pierre blanche (B) et une pierre noire (N). On va considérer qu'elles représentent des unités d'opposition. Autrement dit, B et N s'annulent mutuellement. Cette annulation est un état que j'appellerai neutre et que je représenterai symboliquement par 0 (zéro).
E : Donc un B plus un N donne 0.
P : Pas tout à fait. Quand tu as dit un B PLUS un N, tu sous-entends la notion d'addition. Or, on n'en a pas encore parlé. La seule définition que tu dois retenir, et c'est bien là une définition, c'est qu'un B ET un N s'annulent mutuellement. C'est tout. Par exemple, si on a deux B et deux N, on aura l'équivalent d'un état neutre. Si on a 1000 B et 1000 N , on aura aussi l'équivalent d'un état neutre.
E : Ouais, c'est simple.
P (souriant) : Simple, oui. Mais pas simpliste. Je suis presque convaincu que dans quelques minutes, tu auras oublié cette simple définition.
E (sourcillant) : Oublié? Vous me mettez au défi?
P : On en reparlera le moment venu... En attendant peux-tu me dire ce qu'est la définition d'une addition. Par exemple, que veux dire 3 + 5 ? Attention, je ne te parle pas ici de l'addition chez les entiers mais bien de l'addition chez les nombres naturels.
E : 8. 3+5, c'est 8. C'est bien évident, non ?
P : Je ne te demande pas la réponse, mais de m'expliquer ce que signifie 3 + 5.
E : ???
P : Allons-y concrètement. Supposons que j'ai 3 pommes. 3 + 5 pourrait vouloir dire qu'on ajoute à ces 3 pommes, 5 pommes.
E : Oh! Bien sûr, c'est évident.
P : En fait, ce qui est important de comprendre dans l'addition, c'est que tu ne peux additionner que des nombres qui représentent une même idée. Par exemple, 3 + 5 pourrait aussi signifier «ajouter 5 oranges à 3 pommes», mais dans ce cas on n'obtient ni 8 pommes, ni 8 oranges, mais bien 8 fruits. Autrement dit, le problème est «ajouter 5 FRUITS à 3 FRUITS». Tout ça pour te dire que dans ce qui va suivre, je vais toujours tenir pour acquis qu'on a affaire à des représentants d'une même idée.
E : Ok, ça me va.
P : Bon ! On attaque le vif du sujet. D'abord, on va se donner une convention. Par exemple si j'ai 5 B, je vais symboliser la chose par (+5). Si j'ai 5 N, je vais plutôt utiliser (-5).
E : Donc, un «plus» pour les B, et un «moins» pour les N. Et les parenthèses?
P : Les parenthèses sont là pour indiquer que +5 forme un tout. De même pour -5. On pourrait les enlever, mais je tiens pour l'instant à ce qu'on les garde car on pourra plus facilement distinguer le symbole + qui signifie B du symbole + qui signifie l'addition.
L'enseignant se sentait d'attaque. Il voyait bien que son élève était attentif.
L'élève trouvait la leçon relativement plate jusqu'ici. Il n'avait pas vraiment l'impression d'avoir appris quelque chose de nouveau.
P : Bon, on va maintenant trouver un sens à l'opération addition chez les entiers.
L'enseignant prit 3 pierres blanches dans sa main.
P : Ajoute 5B.
L'élève prit 5 pierres blanches et les ajouta dans la main de l'enseignant.
P : Additionner, c'est ça : ajouter quelque chose à ce qui est déjà là!
E : C'est un peu simplet, votre affaire !
P (avec un grand sourire) : Pourtant, additionner est une opération assez complexe. Par exemple, 345 + 657 + 2302 demande quand même un certain effort pour trouver la réponse. Mais effectivement, l'idée même de l'addition n'est pas très compliquée à saisir. Donc, pour en revenir à notre problème, on pourrait le symboliser ainsi : (+3) + (+5). Note les symboles "+". Il y en a trois. Dans les parenthèses, ils signifient simplement qu'on considère des B. alors que celui du milieu correspond au symbole de l'addition. Il faut donc être très prudent lorsqu'on écrit une telle expression. Et la réponse est ...?
E : La réponse est 8.
P : Non.
E : ???
P : La réponse N'EST PAS 8.
E (en fronçant les sourcils) : Oups ! 8 B ou, symboliquement (+8).
P : Voilà ! Continuons avec ce problème : ajoute 5N à 2N.
L'enseignant a mis 2 pierres noires dans sa main. En haussant les épaules, l'élève prit 5 pierres noires et les ajouta tout simplement.
E : Cela donne 7 N ou, symboliquement (-7).
P : Comment écrirais-tu le tout?
E : (-2) + (-5) = (-7).
P : Parfait. On va compliquer un peu la chose.
L'enseignant prit 2 B dans sa main.
P : Ajoute 5 N à 2 B.
E (en prenant 5 pierres noires et en les ajoutant dans la main de l'enseignant) : Franchement ! C'est pas plus compliqué.
P : Et ça donne?
E : ???
P : Tu te rappelles la définition des nombres entiers, n'est-ce pas?
E (semblant vivre une illumination) : Bien sûr !!!
Et il supprima de la main de l'enseignant 2 couples de pierres noires/blanches.
E : Et voilà, on a 3N soit (-3). Symboliquement, cela s'écrit : (+2) + (-5) = (-3).
P : Très bien ! D'après toi, si on ajoute 15 B à 10 N, qu'est-ce que cela donnerait?
L'élève prit une moue confiante et, après quelques secondes répondit :
E : Cela donne 5 B ou (+5).
P : Pourquoi?
E : ???
P : Dis-moi comment tu as fait dans ta tête pour arriver à ce résultat.
E : J'ai imaginé tout simplement un pot avec 15 pierres blanches et 10 pierres noires. Comme 1 B et 1 N s'éliminent, je peux donc annihiler 10 couples de B/N, et il me restera 5 B dans le pot.
L'enseignant était très heureux : il était convaincu que le concept d'addition était très bien entré dans la tête de son élève. Après l'avoir vérifié avec des exercices oraux, il passa au concept de la soustraction.
P : Bien. On va maintenant apprendre à soustraire. Additionner, c'est AJOUTER des pierres d'une certaine couleur. Soustraire, c'est tout simplement les ENLEVER.
L'enseignant prit 10 blanches dans sa main.
P : Enlève 7 B.
L'élève, qui commençait à s'habituer aux questions simplistes de son enseignant s'exécuta.
E : Et hop là ! il reste 3 B.
P : Effectivement. Symboliquement on a (+10) - (+7) = (+3). C'est un peu enfantin...
E : Je suis bien d'accord avec vous.
P (En prenant 10 N dans sa main) : Ok. Enlève 3 pierres noires.
E (en exécutant la consigne) : Vraiment, y'a rien là. Attendez, je vais vous écrire ce que cela représente symboliquement. (-10) - (-3) = (-7). C'est bizarre, quand je vois l'opération dans ma tête (avec les pierres) il me semble que c'est vraiment une opération niaiseuse. Pourtant, juste avant d'entrer ici, j'y comprenais rien à la soustraction.
P : Attends ! On n'a pas terminé.
Puis, il prit 5 B dans sa main.
P : Enlève 2 pierres noires.
E : ???
P (insistant) : E N L È V E 2 pierres noires.
E : J'peux pas. Vous n'en avez pas dans votre main.
P (souriant) : Si, j'en ai
E (têtu) : Non, il n'y en a pas.
P (regardant l'élève droit dans les yeux) : Regarde comme il faut ! J'AI DES PIERRES NOIRES DANS MA MAIN.
L'élève, croyant que son professeur était en train de devenir fou, secoua la tête. Après quelques secondes, l'enseignant s'enfonça dans le dossier de sa chaise et lui dit :
P : Tu te rappelles au début de la leçon? Je t'avais dit que tu oublierais la définition des entiers. C'est justement ce que tu fais en ce moment. J'ai gagné mon pari.
Encore une fois, l'élève fronça les sourcils et ne comprenait pas ce qu'il se passait. L'enseignant ouvrit sa main qui contenait les 5 pierres blanches.
P : Regarde bien. Il y a dans cette main, une infinité de pierres noires. MAIS TU NE LES VOIS PAS. Elles sont pourtant bien là.
Puisque l'élève ne semblait pas trop saisir les propos de l'enseignant, ce dernier prit un couple de pierres b/n et les déposa dans sa main.
P : Es-tu d'accord pour dire que 5 B, c'est comme 6 B et 1 N, puisque selon la définition des entiers...
E (en coupant l'enseignant) : Ça y est. Je viens de comprendre. C'est comme si vous ajoutiez des zéros. Ce qui dans le fond, ne change rien...
P : C'est ça. On a ce qu'on pourrait appeler des états équivalents. Donc, peux-tu enlever 2 N à mes 5 B?
E (fier de lui) : Bien sûr !
Et il ajoutant aux 5 B deux couples de (B/N). Puis, il prit les 2N. Il restait 7B dans sa main.
E : Symboliquement on a : (+5) - (-2) = (+7). Hé, hé, facile !!!
P : En effet, c'est pas si compliqué que ça. Encore une fois, j'aimerais que tu fasses bien la distinction entre l'opération soustraction symbolisée par un moins. Et le moins qui représente les pierres noires.
E (content de son jeu de mots) : Oui,oui, je vois bien la différence.
P: Ok. Voyons comment tu vas résoudre celui-ci.
L'enseignant mit 5 pierres blanches dans sa main.
P: Enlève 8 pierres blanches.
E (ne trouvant pas le défi tellement difficile) : Bof ! Il suffit d'ajouter ... hum... trois couples B/N. Ainsi, je pourrai soustraire les 8 pierres blanches... Il me restera alors 3 pierres noires. Donc, (+5) - (+8) = (-3). C'est tout de même bizarre de voir apparaître des N alors qu'on enlève des B.
P : Oui. Je suis d'accord avec toi. Il y a comme un brin de magie là-dedans. Mais tout cela ne découle que de la définition, ou si tu veux, de la nature même des nombres entiers. Ils sont vraiment surprenants ! Bon, regarde ce problème.
Et l'enseignant, sur un bout de papier écrit : (-10) - (+1). D'après toi, qu'est-ce que cela donne?
E : Bon, j'ai 10 pierres noires. Je dois enlever une pierre blanche... Bien, il suffit que j'ajoute un seul couple B/N. Si j'enlève maintenant la pierre blanche, il me restera 11 N. Donc, la réponse est (-11).
En résolvant le problème, l'élève manipulait les pierres. C'est ainsi que l'enseignant posa encore quelques questions pour s'assurer que l'idée était bien entrée dans le cerveau de son élève. Puis, il lui demanda.
P : Que donne maintenant cette expression : (-142) - (+99)?
L'élève souriait. Les nombres étaient beaucoup plus gros mais il ne sentait plus la nécessité d'utiliser les pierres.
E : Hum... Je dois enlever les blanches, mais il n'y en a pas dans mes 142 N. Donc, je dois ajouter à ces 142N, 99 couples (B/N). Ainsi, en enlevant les 99 B, je me retrouve avec 99 N de plus, donc... 241 N. Ma réponse : (-241).
La cloche venait de sonner. L'enseignant était fier des progrès de l'élève.

Notes pédagogiques

1. Il faut s'assurer que la notion d'addition chez les naturels est très bien comprise par l'élève. Dans le texte, l'enseignant devrait sans doute appuyer sur le fait qu'on ne peut additionner que des natures semblables (des pommes, des oranges, des fruits.)
2. Le modèle pierre blanche, pierre noire est utile pour l'ensemble des opérations chez les entiers. Par exemple, pour la multiplication, voyez ce billet. Il peut aussi servir à la relation d'ordre. Il permet donc de garder une cohérence dans les explications. On voit souvent l'addition expliquée à partir d'une droite numérique ou comme des comptes bancaires avec un actif et un passif, etc. Pour la soustraction, on noie l'élève dans une règle (soustraire c'est additionner l'opposé!!!!) sortie du chapeau magique de l'enseignant.
3. Il est très important de conserver les parenthèses lorsqu'on initie les élèves aux nombres entiers. Quand on sera assuré que le concept est bien compris, on pourra lui suggérer de supprimer ces parenthèses.
4. Énoncer des règles du genre «si on additionne un entier positif avec un entier négatif, on doit soustraire le plus grand du plus petit et donner le signe du plus grand», c'est prendre l'élève pour un idiot. Il faut que l'élève COMPRENNE les opérations sur les entiers. L'élève qui aura compris le principe de l'addition se fera ses propres règles, s'il en sent le besoin.
5. Laissez tout le temps nécessaire aux élèves de manipuler les pierres. Il faut qu'ils sentent les opérations. Je suggère de toujours associer les manipulations à la représentation symbolique. Éventuellement cette seule représentation symbolique sera suffisante. Encore une fois : laissez le temps aux élèves de manipuler les pierres. Et je répète : laissez le temps aux élèves de manipuler les pierres.

Je plaide pour une renaissance des pratiques ascétiques, pour maintenir vivants nos sens, dans les terres dévastées par le «show», au milieu des informations écrasantes, des conseils à perpétuité, du diagnostic intensif, de la gestion thérapeutique, de l’invasion des conseillers, des soins terminaux, de la vitesse qui coupe le souffle.
Ivan Illich, La perte des sens, Fayard.

Voilà un autre livre sur ma liste des futurs achats.

Via C'est autre chose!

La structure des révolutions scientifiques trainait depuis déjà plusieurs mois sur ma table de chevet. Ce n'est que cette semaine qu'il eut droit à ma lecture. Pour en savoir un peu plus sur Thomas S. Kuhn, vous pouvez vous rendre sur la Stanfort Encyclopedia of Philosophy ou sur Wikipedia. C'est ce billet de Benoit qui m'a fait découvrir ce livre. Vous y trouverez d'ailleurs un lien vers un résumé du bouquin. Évidemment, vous trouverez aussi des citations/extraits sur Au fil de mes lectures, mais pour vous donner un petit avant-goût, en voici deux :

[...] une nouvelle théorie, quelque particulier que soit son champ d'application, est rarement ou n'est jamais un simple accroissement de ce que l'on connaissait déjà. Son assimilation exige la reconstruction de la théorie antérieure et la réévaluation de faits antérieurs, processus intrinsèquement révolutionnaire qui est rarement réalisé par un seul homme et jamais du jour au lendemain. (p.24)

[...] la transition entre deux paradigmes concurrents ne peut se faire par petites étapes, poussée par la logique et l'expérience neutre. [...] il doit se produire d'un coup (mais pas forcément en un instant), ou pas du tout. (p.207)

Cette dernière citation me fait bien plaisir car, comme plusieurs le savent déjà, je ne suis pas un grand adepte de l'apprentissage par petits pas qui, dans l'esprit de plusieurs, mène inexorablement vers un changement dans la pensée du marcheur.

Une lecture conseillée à tous les amateurs de l'évolution de la pensée scientifique et de l'épistémologie.

« [...] ce peut être aussi cela l'existence ! Des miracles parfois, de l'or et des rires, et de nouveau l'espoir quand on croit que tout autour de soi n'est que saccage et silence ! » (p. 159)

À lire absolument, ce court roman de 160 pages nous prend droit au coeur. C'est un texte sur l'absence, le denuement et l'amour. Et sur l'amitié. On pourrait presque dire l'amitié/amour. Et puis on y trouve une belle leçon de communication humaine dans ce livre. Il se lit d'une traite et ne vous laissera pas indifférent. L'histoire? Imaginez un vieillard qui doit fuir son pays et qui se retrouve, désamparé, dans une grande ville dont il ne connaît ni la langue, ni les coutumes de ses habitants. Mais il n'est pas seul : il est avec sa petite fille, Sang Diû (Matin doux) âgée de quelques semaines...

Philippe Claudel, La petite fille de Monsieur Linh, Stock, 2005.

« D'une certaine manière, le mot lecture signifie se perdre dans les fictions d'auteurs comme Scott, Dickens, Cooper, Alger, ou dans les pages d'un catalogue. D'une certaine manière, je paraissais retenir davantage ce que je lisais que ce que j'étudiais. Et je retiens davantage parce que les auteurs que je lis m'emportent hors de ma chambre, hors de moi-même, ce que ne font jamais les auteurs des livres que j'étudie. »
Walter M. Mason, The Wonderful World of Books, Mentor Books, 1952, p. 199.

Dans cette vidéo, Alain Rey nous dévoile l'origine du mot «blog». Vous n'y apprendrez pas grand-chose, mais comme M. Rey mentionne une fois les Québécois....

Obtenu via affordance.info

Il existe une quantité incroyable d'espace vide dans l'univers. La distance du soleil à l'étoile la plus rapprochée est d'environ 4,2 années-lumière, ou 25 suivi de 12 zéros (milles) ... De même pour la masse: le soleil pèse environ 2 suivi de 27 zéros (tonnes) ... La Voie Lactée pèse 160000 fois autant que le soleil; elle est une galaxie parmi une collection d'autres dont environ 30 millions sont connues. Ce n'est pas très facile de retenir une croyance à sa propre importance en regard de statistiques aussi accablantes.
Bertrand Russell

Ce texte est en épigraphe au chapitre intitulé Le sophisme, dans le livre de Vincent Edward Smith, Éléments de logique, Centre de Psychologie et de Pédagogie, 1966. J'ai trouvé ce livre (7$) chez un bouquiniste de Gatineau. Comme vous le savez sans doute, Russell était un éminent logicien, co-auteur, avec Whitehead, du célèbre Principia Mathematica. Voici le commentaire du professeur Smith au regard de l'extrait ci-haut mentionné : « Dans le texte [...], Russell commet le sophisme de l'ignorance du sujet. Ce sophisme consiste à prouver autre chose que la question à prouver et à user de faux-fuyants. Les figures de Russell montrent que le cosmos est immense. Mais elles n'ajoutent ni n'enlèvent rien à la dignité humaine. » p. 282.

Il est très difficile de ne pas tomber dans le piège du paralogisme. Mais en voyant même les plus grands chuter, on se console...

On flanche.
On se relève.
Et on espère gagner un peu plus en sagesse.

J'ai récemment retiré un billet que j'avais publié sur Recit.org. Dans ce billet, j'émettais l'opinion que le discours prononcé à l'ouverture de notre session de travail par le sous-ministre adjoint à l'éducation était «très ordinaire». Suite à sa parution, quelques personnes m'ont signalé leurs malaises par rapport à mon propos. En effet, des commentaires du genre «on ne mord pas la main qui nous nourrit» ou «puisque c'est publié sur le blogue DU Récit, cela donne une mauvaise image du Récit» m'ont été gentiment mentionnés.

Si j'avais laissé le billet sur le blogue, la polémique qu'il aurait pu susciter aurait été sans doute vaine, stérile et inutile. Je fais partie de ceux qui croient que les politiciens sont d'abord à notre service, et non au service de leur Power trip. En ce sens, dire à un politicien que son discours est plutôt plate, c'est lui dire qu'il devrait se forcer pour nous donner un peu plus de viande. Je suis tanné des lieux communs qu'on nous dessert à tour de bras.

Mais de toute évidence, ma vision de l'homme politique n'est pas partagée par une partie de mes confrères et consoeurs du Récit. Et je considère que l'harmonie du groupe est beaucoup plus importante que mon simple point de vue, surtout si ce point de vue est vaguement périphérique à mon travail. Pour bien des gens, il faut user de stratégies avec les politiciens si on veut obtenir quoi que ce soit d'important pour nous. Mais comme je suis allergique à la manipulation, j'ai tendance à me tenir loin des personnes qui en vivent et je me colle plutôt aux gens qui semblent valoriser une certaine profondeur et une certaine rigueur de la pensée. Je ne dis pas que tous les hommes politiques sont vides, je dis seulement qu'ils montrent très peu souvent leur potentiel intellectuel hors les normes établies. J'aimerais du leadership, de l'originalité, du risque, de la transparence. En général, nous n'avons que de l'image, des idées creuses et ramanchées et du conservatisme.

Conclusion : je dois me tenir loin de la politique.

Certains décrivent « Acide sulfurique » comme un roman-scandale ? C'est plutôt l'exercice de rentrée d'une petite dégoûtée qui cherche sa fessée.
Marc Lambron, commentant ici le roman de la rentrée d'Amélie Nothomb.

J'en veux un ! Mais ça doit coûter un bras...