mercredi 15 juin 2005
Beauté III
Par Gilles Jobin, mercredi 15 juin 2005 :: Mathématiqueries
Dans l'excellent Challenging Problems in Geometry de Posamentier et Salkind (Dover, 1996), les auteurs comparent la méthode du paysan et la méthode du poète en matière de résolution de problèmes (peasant's way, poet's way). Pour comprendre ces deux approches, ils donnent un problème semblable à celui-ci :
D'abord, pour bien comprendre le problème énoncé ci-haut, je rappelle que l'inverse d'un nombre x est 1/x. Par exemple, l'inverse de 4 est 1/4 ou 0,25.
La manière paysanne (et telle fut d'ailleurs mon approche !) de faire les choses est la suivante :
Posons le système d'équations
x + y = 7
et
xy = 8
Par simple substitution, cela revient à résoudre l'équation du second degré : 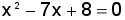 . De là, on trouve facilement x et, par la suite y. Il suffit ensuite d'additionner l'inverse de ces nombres. (Ici,
. De là, on trouve facilement x et, par la suite y. Il suffit ensuite d'additionner l'inverse de ces nombres. (Ici, 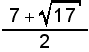 et
et 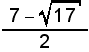 sont les deux nombres.) La somme des inverses de ces nombres donne 7/8, qui est la réponse cherchée. Si vous faites correctement toutes les étapes, elles peuvent facilement vous demander une quinzaine de minutes de concentration.
sont les deux nombres.) La somme des inverses de ces nombres donne 7/8, qui est la réponse cherchée. Si vous faites correctement toutes les étapes, elles peuvent facilement vous demander une quinzaine de minutes de concentration.
Voyez maintenant la méthode dite du poète :
On cherche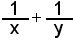 . Or, algébriquement parlant, si on fait l'addition, on a
. Or, algébriquement parlant, si on fait l'addition, on a 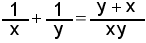 . Et, sans connaître x ni y, on sait que cela correspond à 7/8, car la somme (7 dans la donnée du problème) est au numérateur et le produit (8 dans la donnée du problème) est au dénominateur ! La réponse est trouvée en quelques secondes, et, ma foi, d'une manière fort élégante. Autrement dit, la solution ne passait pas nécessairement par la découverte des deux nombres en question.
. Et, sans connaître x ni y, on sait que cela correspond à 7/8, car la somme (7 dans la donnée du problème) est au numérateur et le produit (8 dans la donnée du problème) est au dénominateur ! La réponse est trouvée en quelques secondes, et, ma foi, d'une manière fort élégante. Autrement dit, la solution ne passait pas nécessairement par la découverte des deux nombres en question.
Voyez maintenant ce petit problème très cher à mon collègue philosophe Mario :
(Paesant's way) :
Ronde 1 : 60 parties
Ronde 2 : 30 parties
Ronde 3 : 15 parties
Ronde 4 : 7 parties (reste un joueur qui a un bye)
Ronde 5 : 4 parties.
Ronde 6 : 2 parties.
Ronde 7 : 1 partie.
Donc, on doit disputer 119 parties.
(Poet's way)
Une partie élimine un joueur. Il faut éliminer 119 joueurs. Donc 119 parties seront nécessaires !!!
Petite question : Qu'arriverait-il si je donnais le premier problème à résoudre à des enseignants du primaire? Je vous laisse deviner les réactions. Ne serait-ce point là une belle manière d'aborder les émotions en maths !
Trouvez la somme des inverses des nombres dont la somme est 7 et le produit est 8.Pour ceux d'entre vous qui ne sont pas du tout matheux, je vous prierais de continuer tout de même la lecture, quitte à sauter les côtés trop mathématiques de la solution. En effet, mon but n'est pas ici de faire des maths, mais de vous faire plutôt ressentir une belle solution, même si les connaissances exigeant cette résolution vous font défaut. Et puis, à la toute fin du billet, vous pourrez tenter un petit problème beaucoup plus simple et dont la solution n'exige aucune habileté mathématique. Ce problème illustrera un autre exemple de la paysannerie versus la poésie.
D'abord, pour bien comprendre le problème énoncé ci-haut, je rappelle que l'inverse d'un nombre x est 1/x. Par exemple, l'inverse de 4 est 1/4 ou 0,25.
La manière paysanne (et telle fut d'ailleurs mon approche !) de faire les choses est la suivante :
Posons le système d'équations
et
xy = 8
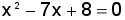 . De là, on trouve facilement x et, par la suite y. Il suffit ensuite d'additionner l'inverse de ces nombres. (Ici,
. De là, on trouve facilement x et, par la suite y. Il suffit ensuite d'additionner l'inverse de ces nombres. (Ici, 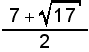 et
et 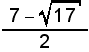 sont les deux nombres.) La somme des inverses de ces nombres donne 7/8, qui est la réponse cherchée. Si vous faites correctement toutes les étapes, elles peuvent facilement vous demander une quinzaine de minutes de concentration.
sont les deux nombres.) La somme des inverses de ces nombres donne 7/8, qui est la réponse cherchée. Si vous faites correctement toutes les étapes, elles peuvent facilement vous demander une quinzaine de minutes de concentration.
Voyez maintenant la méthode dite du poète :
On cherche
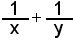 . Or, algébriquement parlant, si on fait l'addition, on a
. Or, algébriquement parlant, si on fait l'addition, on a 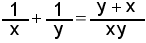 . Et, sans connaître x ni y, on sait que cela correspond à 7/8, car la somme (7 dans la donnée du problème) est au numérateur et le produit (8 dans la donnée du problème) est au dénominateur ! La réponse est trouvée en quelques secondes, et, ma foi, d'une manière fort élégante. Autrement dit, la solution ne passait pas nécessairement par la découverte des deux nombres en question.
. Et, sans connaître x ni y, on sait que cela correspond à 7/8, car la somme (7 dans la donnée du problème) est au numérateur et le produit (8 dans la donnée du problème) est au dénominateur ! La réponse est trouvée en quelques secondes, et, ma foi, d'une manière fort élégante. Autrement dit, la solution ne passait pas nécessairement par la découverte des deux nombres en question.
Voyez maintenant ce petit problème très cher à mon collègue philosophe Mario :
120 élèves se présentent à un tournoi scolaire de ping-pong. Seuls des matchs simples sont disputés. À chaque match, l'élève perdant est éliminé et le vainqueur continue jusqu’à ce qu’il ne reste plus qu’un seul grand gagnant. Combien de parties seront jouées ?Pensez-y quelques minutes. Puis, regardez les deux solutions ci-dessous:
(Paesant's way) :
Ronde 1 : 60 parties
Ronde 2 : 30 parties
Ronde 3 : 15 parties
Ronde 4 : 7 parties (reste un joueur qui a un bye)
Ronde 5 : 4 parties.
Ronde 6 : 2 parties.
Ronde 7 : 1 partie.
Donc, on doit disputer 119 parties.
(Poet's way)
Une partie élimine un joueur. Il faut éliminer 119 joueurs. Donc 119 parties seront nécessaires !!!
Pour finir
En ce qui concerne le premier problème, la méthode paysanne exige une bonne technique mathématique. Si vous avez réussi dans votre vie un cours de niveau 4e secondaire, vous avez tous les outils pour le résoudre de cette manière. Cependant, je suis à peu près convaincu que même si vous avez réussi ce cours avec une très bonne note, vous avez sans doute bloqué à un moment ou à un autre. Pourquoi ? Tout simplement parce que les techniques enseignées au secondaire non seulement s'oublient, mais elles sont à peu près complètement inutiles au commun des mortels. Or, vous en avez probablement fait des tonnes de problèmes tels celui des deux nombres. Tout ce qu'on a sans doute réussi à faire avec ces exercices, c'est de vous donner une bonne écoeurite des mathématiques. C'est pourquoi je milite pour un arrêt de l'enseignement des maths au secondaire. J'irais même jusqu'à dire que cet enseignement nuit à l'essor de la pensée logico-mathématique chez les enfants. D'après moi, l'école crée beaucoup plus de mathophobes que de logicophiles! Il est vrai que la solution du poète demande aussi une connaissance mathématique (addition de fractions algébriques.) En fait, la beauté ici ne réside pas du tout dans la question qui est, scolairement parlant, assez banale, mais plutôt dans le HAHA de sa solution poétique. Certains qui aiment les maths aiment aussi ces twists intellectuels.Petite question : Qu'arriverait-il si je donnais le premier problème à résoudre à des enseignants du primaire? Je vous laisse deviner les réactions. Ne serait-ce point là une belle manière d'aborder les émotions en maths !

