Le merveilleux dans les nombres se trouve
dans les nombres eux-mêmes !
Pas la peine de les plomber de
desseins mystico-psychologiques.
Denis Guedj, Le théorème du perroquet.
Averstissement : Désolé pour la longueur du texte. Je me suis tellement amusé à l'écrire que je ne pouvais pas ne pas en laisser la trace ici. G.J.
L'enseignant circulait entre les bureaux. Il n'y avait que quelques élèves à cette session de récupération.
ENS : Tu es dans la loi des signes, fit-il en regardant par-dessus l'épaule d'un élève sa feuille de travail.
ELE : Ouais...
Le manque d'enthousiasme de l'élève ne l'étonnait pas. Après tout, faire une série d'exercices sans trop comprendre est un acte plutôt abrutissant ayant peu de noblesse. Il tenta une question.
ENS : Sais-tu pourquoi le produit de deux négatifs donne un positif ?
ELE : C'est juste une loi, répondit-il en pointant du crayon un encadré sur la page de son livre.
ENS : Et tu crois cette loi... juste ?
L'élève souleva un sourcil. Cet enseignant avait la réputation d'être plutôt excentrique.
ELE : Juste ?
ENS : C'est bien ma question. Est-ce un loi «juste» ?
ELE (en haussant les épaules) : C'est écrit dans le livre, elle doit être vraie !
ENS : Une loi ... vraie??? T'as déjà entendu parler d'une loi vraie???
L'enseignant approcha une chaise du bureau de l'élève et s'y installa confortablement. Tout était tranquille dans la classe.
ENS (calmement) : Dis-moi. D'après toi, d'où vient-elle cette loi?
ELE : Des mathématiciens, c'est certain.
ENS : Et les mathématiciens, ils l'ont prise où, cette loi?
ELE : Ils l'ont inventée, probablement.
ENS : Inventée ? Ils ont inventé une loi ? Une loi qui est vraie?
ELE (désorienté): Je suppose.
ENS : D'après toi, comment pourrait-on vérifier si cette loi est vraie?
ELE (sarcastique) En allant voir les réponses à mes exercices !!!
ENS (en souriant) : Mais encore ?
ELE : Je sais pas trop. On m'a toujours dit que multiplier deux moins donne un plus. Alors, je vois pas pourquoi je me poserais la question du pourquoi du comment de la chose. Ça fonctionne comme ça, c'est tout. Les maths, pour moi, c'est juste des lois qu'on doit se mettre dans la tête et qu'on doit appliquer quand le prof nous dit de le faire.
ENS : Tu es un élève bien docile.
ELE : J'ai pas le choix. Faut bien que je les réussisse ces foutues mathématiques.
ENS : Si je comprends bien, pour toi, réussir signifie «
dire comme le prof.»
ELE : Faut bien !
ENS : Tu suis donc les consignes du prof, sans rien comprendre c'est bien ça ?
Hochement de tête.
ENS : Et si tu arrivais à comprendre vraiment que deux moins donne un plus ...
ELE (coupant le prof ) Y'a rien à comprendre. C'est une loi. C'est tout.
ENS (tentant de sonder l'âme de l'élève) : C'est tranquille dans la classe. Qu'en penses-tu si, pour une fois, tu ne croyais pas le prof, mais que tu essayais de comprendre par toi-même ? Je peux t'aider à comprendre si tu veux.
ELE (Haussement d'épaule) J'ai jamais rien compris aux maths, alors...
ENS Pourtant, tout le monde peut comprendre les maths.
Et l'enseignant écrivit sur un bout de papier : 2 x 5.
ELE : 10 !
ENS : Bravo , tu connais tes tables. Sans blague, qu'est-ce que je viens d'écrire?
ELE : ???
L'enseignant pointa le deux et dit DEUX puis il pointa la x et attendit que l'élève parle :
ELE : deux fois cinq. Ça donne 10. C'est vraiment élémentaire.
ENS : Je suis bien d'accord que deux fois cinq donne 10. Mais j'aimerais savoir si tu SAIS ce que le "fois" veut dire.
ELE : Deux fois cinq, ça veut juste dire cinq plus cinq. On a deux fois le nombre cinq. C'est simple.
ENS : Bravo ! Vois-tu une différence si j'avais lu «
deux MULTIPLIÉ par cinq ? »
ELE : Ç'est pareil. Ça donne 10 aussi?
ENS : C'est
pareil??? insista le prof.
ELE : Bien, ça veut dire «
deux plus deux plus deux plus deux plus deux.» Mais ça donne la même réponse.
L'enseignant était content. Le concept de multiplication était bien installé chez l'élève. Il fallait maintenant lui faire prendre conscience d'une subtilité importante.
ENS : Es-tu d'accord que
deux fois cinq pourrait représenter quelque chose comme
deux fois un billet de cinq dollars?
ELE : Oui, je suis d'accord. Ou encore cinq fois une pièce de deux dollars.
ENS : Exactement. Mais dans les deux cas, c'est un peu comme si on avait deux catégories de nombres : un type qui représente l'objet et un autre qui représente le nombre de fois qu'on a cet objet.
Et l'enseignant dessina :
5$ 5$
deux fois
Le «
deux» et le
5 n'ont pas la même signification, n'est-ce pas?
ELE (qui ne voyait pas trop où voulait en venir l'enseignant) Exact.
ENS (insistant) : Pourtant, on a bien deux nombres
NATURELS. On multiplie ensemble deux nombres naturels
qui ne représentent pas la même réalité. Dans un cas, on a
vraiment 5$ alors que le nombre naturel deux indique tout simplement le nombre de fois qu'on doit additionner ce 5$.
ELE (comme s'il s'attendait à un piège) : Il me semble que tout cela va de soi.
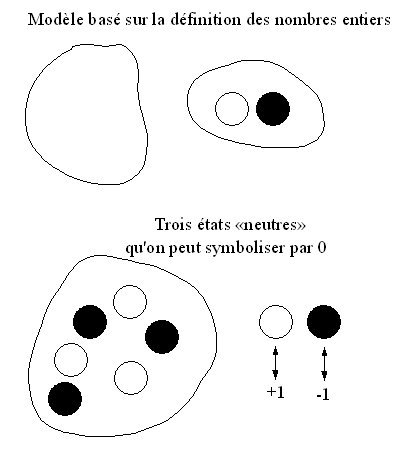
ENS : Ok. Passons dans un autre monde. Celui des nombres entiers. Tu sais, les positifs et les négatifs. Ce monde-là est bien spécial, car une seule et unique règle les régit. Cette règle est d'une grande simplicité. Elle dit la chose suivante : Si on a une même quantité de nombres négatifs et de nombres positifs alors on a l'équivalent d'un état neutre. Par exemple, +2 et -2 donne un état neutre car j'ai la même quantité de «+» que de «-». De plus, le neutre est souvent symbolisé par zéro.
ELE : Mais y'a aussi la loi des signes...
ENS (coupant raide l'élève) : Non, il n'y a pas de loi des signes. Il n'y a QUE cette règle. Tout le reste est déduction logique.
ELE : ???
ENS : Tu m'as bien compris : ces lois sont ridicules. Et tu verras qu'après avoir COMPRIS, tu n'en auras pas besoin.
ELE : ???
ENS : Je vais faire un peu de maïeutique avec toi, tu veux bien?
ELE : Ta... ïeutique???
ENS : Maïeutique. C'était un procédé utilisé par Socrate, un bon gars mais il est mort maintenant... Par du questionnement, tu vas découvrir par toi-même que deux moins donne un plus. Autrement dit, tu
sais que deux moins donnent un plus. Il suffit juste que tu en prennes conscience !
Les autres élèves de la classe écoutaient la conversation. Plus personne ne faisait les exercices de récupération.
ELE : Ouais...
ENS : Tu connais le jeu de GO?
ELE : ???
ENS : C'est un jeu très joué en Orient. Le Go est à l'Orient ce que le jeu d'échecs est à l'Occident. Dans ce jeu, il y a des pierres blanches et des pierres noires. J'en traîne toujours sur moi.
Et il sortit de ses poches quelques dizaines de pierres blanches et noires. L'élève était stupéfait.
ENS (en déployant les pierres sur la table) : C'est bien pratique pour expliquer les choses. Tu es prêt?
 ELE
ELE : Oui.
ENS : Ok. Pour les besoins de la cause, je vais imaginer qu'une bille blanche représente un entier positif et une bille noire représente un entier négatif.
L'enseignant mis alors dans sa main deux billes blanches et deux billes noires. Puis, sans crier gare, il les lança par-dessus son épaule, pour s'en débarrasser. Il rouvrit la main et dit :
ENS : Voilà le neutre.
Tous les élèves se bidonnaient dans la classe car en lançant les pierres, l'enseignant en avait presque atteint un.
ELE (qui pensait avoir été frappé par un éclair de génie) : Hé, hé, vous voulez dire que +2 et -2, c'est 0!
ENS : Et oui. Symboliquement, on pourrait écrire : +2 + -2 = 0. Mais attention, le «+» du +2 n'a pas du tout le même sens que le + qui vient entre les deux entiers...
ELE (coupant le prof) Oui, oui, je vois bien, le premier PLUS veut dire
bille blanche alors que l'autre veut dire
addition.
ENS : C'est bien ça. En mathématique, on utilise assez souvent un même symbole qui représente des idées différentes. Il faut toujours se méfier.
ELE : Se méfier ? On ne m'a jamais dit ça...
ENS : Je te donnerai des exemples un autre jour si tu veux. Mais là, continuons.
L'enseignant ouvre sa main. Elle est vide.
ENS : Que vois-tu?
ELE : Rien.
ENS : Rien???
ELE : Rien.
ENS : Fais un effort d'imagination. Transporte-toi dans le monde des nombres entiers. (L'enseignant montre toujours la paume de sa main)
ELE : Je vois votre main, c'est tout.
ENS : Moi, je vois du neutre.
Et il mit dans sa paume 4 billes blanches et 4 billes noires.
ENS : Voici aussi du neutre.
Et il mit dans sa paume 10 billes blanches et 10 billes noires.
ENS : Voici encore du neutre. Tu as raison, tout ça, c'est rien (et il jeta rapidement les pierres). Oui, tout ça, c'est la même chose, du neutre seulement du neutre.
Tout le monde riait aux éclats dans la classe.
ENS : Dans le monde des entiers, RIEN peut prendre PLUSIEURS formes. Ne l'oublie jamais. C'est la SEULE et UNIQUE règle de ce monde. Cette seule règle IMPLIQUE que la multiplication de deux nombres négatifs donne un nombre positif.
ELE : Je ne comprends pas trop
pourquoi vous dites cela.
L'enseignant était content. Il venait de frapper fort. L'élève était CURIEUX de connaître la suite.
ENS : Les mathématiciens aiment ÉTENDRE des concepts. Par exemple, dans la multiplication, on a bien vu tantôt que le nombre à gauche du «
fois» n'avait pas du tout le même sens que le nombre à droite.
ELE : Oui, oui, je me rappelle.
ENS : Ok. Écrivons donc -2 x -5.
ELE (jetant un regard sur l'encadré de son livre) : PLUS 10 !
ENS : Ouais... toujours tes règles. Mais cette fois, tu vas trouver logiquement la réponse. Il faut d'abord trouver un sens à l'expression.
ELE : Si je me fie à votre définition, -2 x -5, c'est deux billes noires multipliées par cinq billes noires. Et ça devrait donner, because mon livre de maths, 10 billes blanches. Franchement, les mathématiciens sont fous !
ENS (joyeux) : Je pense aussi qu'ils ont un grain de folie en eux. La folie de comprendre et de symboliser le monde. Pourquoi diable dis-tu que l'expression représente deux billes noires fois deux billes noires? Alors que dans 2 x 5, tu m'as bien dit tantôt que le nombre à gauche du fois...
ELE (coupant le profs) : Attendez ! Hum... ! C'est vrai que le -2, dans -2 x -5, devrait peut-être dire autre chose... Mais je vois pas trop... Dans 2 x 5, on a additionne deux fois cinq, mais dans -2 x -5... hum... le moins cinq, pourraient signifier cinq billes noires, mais le moins deux...
Et l'éleve continuait de marmonner. Il cherchait un sens à ce moins 2. Les autres élèves s'étaient mis aussi de la partie.
ENS : Une chose demeure certaine, on doit chercher un nouveau sens à ce symbole moins qui précède le deux. Et ce sens doit respecter le principe des entiers (+1 et -1 donne le neutre). Je te suggère le sens suivant : + pourrait dire DONNER et - pourrait dire RETIRER. Cette idée est cohérente avec le principe des entiers : donner 2 et retirer 2 correspondant à un état
neutre. Donner 10, et retirer 10 correspond à un état neutre, etc.
ELE : ???
ENS : Par exemple, +2 x +5 pourrait signifier
DONNER deux fois 5 billes blanches. Ce qui correspond à 10 billes blanches, soit +10. Que voudrait dire +2 x -5?
ELE : Hum... donner deux fois 5 billes noires, donc on aurait 10 billes noires, soit symboliquement -10.
ENS : Tu viens donc de découvrir que
UN PLUS FOIS UN MOINS DONNE UN MOINS. Donne maintenant un sens à -2 x +5.
ELE (hésitant) : Hum... retirer deux fois cinq billes blanches. C'est ridicule, non?
ENS (très heureux, ouvre sa main ) : Que vois-tu?
ELE : ???
ENS : Ne vois-tu pas le neutre?
ELE : Oh! bien sûr.
ENS : Retire s'y deux fois cinq billes blanches.
ELE : C'est ce que je disais tantôt, c'est ridicule.
ENS (insistant) : Allez, tu peux y arriver. Retire deux fois cinq billes blanches.
ELE : Je peux pas. Y'a pas de billes blanches !!!
Un autre élève de la classe s'est alors approché. Il a pigé plusieurs noires et plusieurs blanches du jeux de go, et les a déposé dans la main. Il avait en fait déposé 10 pierres noires et 10 pierres blanches.
ENS (très heureux) : Que vois-tu?
ELE (illuminé) : Je vois le neutre, puisqu'il y a la même quantité de billes blanches que de billes noires. Mais là, JE PEUX retirer deux fois cinq billes blanches. Et il me restera 10 billes noires. Donc -10 !!!
ENS : Et maintenant, comment peux-tu interpréter -2 x -5?
ELE : C'est comme ce qu'on vient de faire, mais cette fois, en retirant les billes noires, ce sont des billes blanches qui resteront !
ENS : Voilà ! Comprends-tu maintenant que la loi des signes, on n'en a pas besoin?
La cloche annonçant le prochain cours venait de sonner. En regardant les élèves quitter la classe, l'enseignant aurait tant voulu les retenir pour leur parler de soustraction, de division et de tout le reste. Il aurait aimé les laisser avec la question de l'ordre de grandeur. Par exemple, de +2 et de -2, lequel est le plus grand? Mais cela viendrait peut-être une prochaine fois.


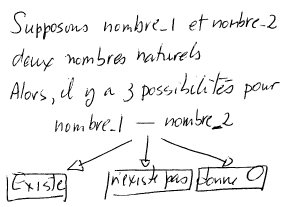 Supposons deux nombres naturels (on va les appeler nombre_1 et nombre_2 pour la cause.)
Supposons deux nombres naturels (on va les appeler nombre_1 et nombre_2 pour la cause.)



.png)