Jobineries

Lu sur Matinternet ce matin :

Prix de l'essence (en moyenne): 0,99.4 $ /litre d'ordinaire.
On comprend tous le sens de la phrase, mais le prof de math en moi se demande bien comment expliquer une pareille notation aux élèves...

Mon oncle Jacques vient tout juste de me signaler la découverte du plus grand nombre premier à ce jour. Pour rappel, un nombre premier n'est divisible que par lui-même et par 1. Par exemple, 29 est un nombre premier car on ne peut le diviser que par 29 ou par 1. 39 ne l'est pas étant divisible par 1, 3, 13 et 39.

Depuis Euclide, on sait qu'il y a une infinité de nombres premiers. La nouvelle de CNN nous apprend qu'à la mi-décembre, une équipe de la Central Missouri State University a découvert un nombre de 9,152,052 chiffres qui était premier. Ce nombre fait partie de la catégorie dite nombre de Mersenne. Un nombre de Mersenne en est un de la forme 2^p-1 où p est un nombre naturel. Par exemple : 2¹⁰-1 = 1023 est un nombre de Mersenne.

Vous trouverez ici la liste des 42 plus petits nombres premiers de Mersenne connus en 2005 (excluant ce M30402457 = 2^30402457-1). Tous les détails sur le site officiel consacré à la recherche des nombres de Mersenne premiers.

La vulgarisation c'est le « fait d'adapter des notions, des connaissances scientifiques ou techniques afin de les rendre compréhensibles au non-spécialiste; reformulation d'un discours spécialisé qui consiste généralement à le débarrasser de ses difficultés spécifiques, de ses caractères techniques afin de le rendre accessible au grand public. » (Trésor de la Langue Française Informatisé)

Dans cet esprit, croyez-vous possible de vulgariser des idées, des concepts mathématiques ? Prenons par exemple les logarithmes. Je suis à peu près convaincu que pour plusieurs d'entre vous, la seule évocation du mot vous dresse les cheveux sur la tête. D'ailleurs, vous êtes peut-être immédiatement passé en mode «J'aiJamaisRienComprisAuxMaths/JeSuisPocheEnMaths». Si c'est votre cas, je tenterai d'expliquer la notion de logarithme pour diminuer un peu cette réticence. Ou, peut-être, êtes-vous soudainement devenu curieux? Dans ce cas, ma vulgarisation vous incitera-t-elle à aller un peu loin? Réussirais-je dans mon explication?

Un logarithme, c'est une drôle de bibite. Bibite elle-même très liée à une autre qu'on appelle un exposant. Ne paniquez pas ! Ce n'est pas si difficile que cela en a l'air. Voyez plutôt :

2 x 2 x 2 = 8.

Les mathématiciens, naturellement très paresseux, préfèrent écrire 2³=8.
Dans leur langage, ils appellent ça la notation exponentielle. Dans ce cas, l'exposant est 3. Quant au 2, on lui donne le nom de base. Ils diront par exemple, 2 exposant 3 donne 8. Un autre exemple : 4 exposant 5 donne 1024 qu'on notera ainsi : 4⁵=1024. Certains disent aussi : 2 élevé à la troisième puissance donne 8, 4 élevé à la cinquième puissance donne 1024. Ou, plus simplement, 2 puissance 3 donne 8; 4 puissance 5 donne 1024.

Est-il possible de donner un sens à une expression du genre 4^1,2 ou encore une expression dont l'exposant serait un entier négatif comme 5^-3? La réponse est affirmative mais l'explication sort du propos de ce billet.

Le logarithme décrit autrement cette même idée. Il a en effet fallu inventer ce mot lorsqu'on désira énoncer l'expression en «partant» de l'exposant.
Dans le premier exemple ci-haut, «2 exposant 3 donne 8», on énonce l'égalité à partir de la base (2 exposant bla-bla-bla). Or, si on désire partir de l'exposant, on dira plutôt : 3 est le logarithme de 8 en base 2. Et, juste pour faire paniquer les non-initiés, ils notèrent la chose ainsi : 3 = log₂8. On peut aussi lire cette expression ainsi : 3 est l'exposant qu'il faut que je donne à 2 pour obtenir 8. D'autres diront plutôt «3 est le log de 8 en base 2».
Le deuxième exemple pourrait s'écrire : 5 = log₄1024. Autrement dit, 5 est l'exposant qu'il faut que je donne à 4 pour obtenir 1024. Ou encore : « Le log de 1024 en base 4 est 5 ».

La notation exponentielle et la notation logarithmique ne sont que deux styles pour décrire une même idée mathématique.

---

Peut-on parler ici de vulgarisation ? Si oui, est-elle réussie ? Si vous connaissiez déjà la notion présentée, trouvez-vous que ce texte en dénature l'esprit ?

Les casse-tête sudoku sont extrêmement populaires par les temps qui courent. J'aimerais cependant attirer votre attention sur un autre type d'énigmes qui, ma foi, existent depuis une bonne dizaine d'année.

En américain, on les appelle des cross sums. Vous en trouverez plus de vingt (du plus facile au plus difficile) à chaque parution du magazine Dell Math Puzzles and Logic Problems. Ci-dessous, le problème no. 13 de l'édition du mois de novembre. (Désolé pour la numérisation. Je crois cependant que l'image est suffisamment claire pour vous donner une bonne idée du problème.)



Les règles sont simples :
1. Vous devez remplir les espaces blancs par un chiffre de 1 à 9.
2. Chaque combinaison de chiffres doit s'additionner pour donner le résultat à gauche pour une combinaison horizontale et au-dessus pour une combinaison verticale.
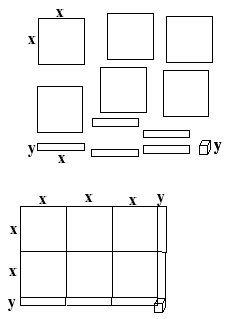
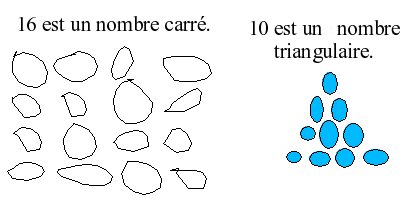
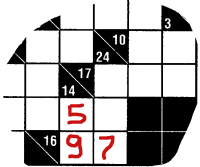3. Vous ne pouvez réutiliser le même chiffre dans une même combinaison. Par exemple, si vous devez trouver deux chiffres qui donnent 16, (comme en bas et à droite de l'image), vous pouvez inscrire soit 7 et 9, ou 9 et 7, mais non 8 et 8. Donc, la seule combinaison possible (pour le 16 qui est en bas et à droite de l'image) est 9 et 7, car si on mettait 7 et 9, on ne pourrait compléter la somme verticale qui doit donner 14, car cela impliquerait une combinaison de 7 et 7.

Les cases entourées de gris vers le centre de la grille n'ont pas d'importance. Elles entourent une combinaison donnée un peu plus loin dans le magazine pour aider ceux qui en ressentent le besoin.

P représente l'enseignant et E, l'élève.

Contexte : l'élève doit passer une heure en cours de récupération avec un enseignant car on a détecté qu'il avait un sérieux problème de compréhension de l'addition et de la soustraction chez les entiers.

P : On va commencer par faire un petit résumé de ce que sont les entiers.
E (haussant les épaules): Les nombres entiers ? Bof, ce sont les plus et les moins...
P (sentant qu'il aura du plaisir avec son élève) : Hum... En fait, c'est beaucoup plus simple que ça. Les nombres entiers représentent des quantités qui peuvent avoir un opposé. Par exemple, les couples (gagner, perdre), (avancer,reculer), (monter, descendre), (électron, positron)...
E (coupant l'enseignant) : C'est quoi un positron?
P (content de recevoir cette question) : En quelque sorte, c'est le contraire d'un électron. En fait, si tu colles un électron à un positron il en résultera, grosso modo, une annihilation. C'est comme s'ils disparaissaient. En réalité, il résulte de cet affrontement une espèce d'énergie radiante.
E (hésitant): L'antimatiere ?
P (de plus en plus heureux de travailler avec cet élève) : Exactement! Les nombres entiers sont là pour représenter, en quelque sorte, l'idée d'opposition. Pour bien illustrer la chose, je vais prendre un modèle qui devrait t'aider à comprendre comment tout cela fonctionne.
L'enseignant sortit son jeu de go contenant des pierres blanches et des pierres noires. Puis il lui expliqua :
P : Tu vois, on a ici une pierre blanche (B) et une pierre noire (N). On va considérer qu'elles représentent des unités d'opposition. Autrement dit, B et N s'annulent mutuellement. Cette annulation est un état que j'appellerai neutre et que je représenterai symboliquement par 0 (zéro).
E : Donc un B plus un N donne 0.
P : Pas tout à fait. Quand tu as dit un B PLUS un N, tu sous-entends la notion d'addition. Or, on n'en a pas encore parlé. La seule définition que tu dois retenir, et c'est bien là une définition, c'est qu'un B ET un N s'annulent mutuellement. C'est tout. Par exemple, si on a deux B et deux N, on aura l'équivalent d'un état neutre. Si on a 1000 B et 1000 N , on aura aussi l'équivalent d'un état neutre.
E : Ouais, c'est simple.
P (souriant) : Simple, oui. Mais pas simpliste. Je suis presque convaincu que dans quelques minutes, tu auras oublié cette simple définition.
E (sourcillant) : Oublié? Vous me mettez au défi?
P : On en reparlera le moment venu... En attendant peux-tu me dire ce qu'est la définition d'une addition. Par exemple, que veux dire 3 + 5 ? Attention, je ne te parle pas ici de l'addition chez les entiers mais bien de l'addition chez les nombres naturels.
E : 8. 3+5, c'est 8. C'est bien évident, non ?
P : Je ne te demande pas la réponse, mais de m'expliquer ce que signifie 3 + 5.
E : ???
P : Allons-y concrètement. Supposons que j'ai 3 pommes. 3 + 5 pourrait vouloir dire qu'on ajoute à ces 3 pommes, 5 pommes.
E : Oh! Bien sûr, c'est évident.
P : En fait, ce qui est important de comprendre dans l'addition, c'est que tu ne peux additionner que des nombres qui représentent une même idée. Par exemple, 3 + 5 pourrait aussi signifier «ajouter 5 oranges à 3 pommes», mais dans ce cas on n'obtient ni 8 pommes, ni 8 oranges, mais bien 8 fruits. Autrement dit, le problème est «ajouter 5 FRUITS à 3 FRUITS». Tout ça pour te dire que dans ce qui va suivre, je vais toujours tenir pour acquis qu'on a affaire à des représentants d'une même idée.
E : Ok, ça me va.
P : Bon ! On attaque le vif du sujet. D'abord, on va se donner une convention. Par exemple si j'ai 5 B, je vais symboliser la chose par (+5). Si j'ai 5 N, je vais plutôt utiliser (-5).
E : Donc, un «plus» pour les B, et un «moins» pour les N. Et les parenthèses?
P : Les parenthèses sont là pour indiquer que +5 forme un tout. De même pour -5. On pourrait les enlever, mais je tiens pour l'instant à ce qu'on les garde car on pourra plus facilement distinguer le symbole + qui signifie B du symbole + qui signifie l'addition.
L'enseignant se sentait d'attaque. Il voyait bien que son élève était attentif.
L'élève trouvait la leçon relativement plate jusqu'ici. Il n'avait pas vraiment l'impression d'avoir appris quelque chose de nouveau.
P : Bon, on va maintenant trouver un sens à l'opération addition chez les entiers.
L'enseignant prit 3 pierres blanches dans sa main.
P : Ajoute 5B.
L'élève prit 5 pierres blanches et les ajouta dans la main de l'enseignant.
P : Additionner, c'est ça : ajouter quelque chose à ce qui est déjà là!
E : C'est un peu simplet, votre affaire !
P (avec un grand sourire) : Pourtant, additionner est une opération assez complexe. Par exemple, 345 + 657 + 2302 demande quand même un certain effort pour trouver la réponse. Mais effectivement, l'idée même de l'addition n'est pas très compliquée à saisir. Donc, pour en revenir à notre problème, on pourrait le symboliser ainsi : (+3) + (+5). Note les symboles "+". Il y en a trois. Dans les parenthèses, ils signifient simplement qu'on considère des B. alors que celui du milieu correspond au symbole de l'addition. Il faut donc être très prudent lorsqu'on écrit une telle expression. Et la réponse est ...?
E : La réponse est 8.
P : Non.
E : ???
P : La réponse N'EST PAS 8.
E (en fronçant les sourcils) : Oups ! 8 B ou, symboliquement (+8).
P : Voilà ! Continuons avec ce problème : ajoute 5N à 2N.
L'enseignant a mis 2 pierres noires dans sa main. En haussant les épaules, l'élève prit 5 pierres noires et les ajouta tout simplement.
E : Cela donne 7 N ou, symboliquement (-7).
P : Comment écrirais-tu le tout?
E : (-2) + (-5) = (-7).
P : Parfait. On va compliquer un peu la chose.
L'enseignant prit 2 B dans sa main.
P : Ajoute 5 N à 2 B.
E (en prenant 5 pierres noires et en les ajoutant dans la main de l'enseignant) : Franchement ! C'est pas plus compliqué.
P : Et ça donne?
E : ???
P : Tu te rappelles la définition des nombres entiers, n'est-ce pas?
E (semblant vivre une illumination) : Bien sûr !!!
Et il supprima de la main de l'enseignant 2 couples de pierres noires/blanches.
E : Et voilà, on a 3N soit (-3). Symboliquement, cela s'écrit : (+2) + (-5) = (-3).
P : Très bien ! D'après toi, si on ajoute 15 B à 10 N, qu'est-ce que cela donnerait?
L'élève prit une moue confiante et, après quelques secondes répondit :
E : Cela donne 5 B ou (+5).
P : Pourquoi?
E : ???
P : Dis-moi comment tu as fait dans ta tête pour arriver à ce résultat.
E : J'ai imaginé tout simplement un pot avec 15 pierres blanches et 10 pierres noires. Comme 1 B et 1 N s'éliminent, je peux donc annihiler 10 couples de B/N, et il me restera 5 B dans le pot.
L'enseignant était très heureux : il était convaincu que le concept d'addition était très bien entré dans la tête de son élève. Après l'avoir vérifié avec des exercices oraux, il passa au concept de la soustraction.
P : Bien. On va maintenant apprendre à soustraire. Additionner, c'est AJOUTER des pierres d'une certaine couleur. Soustraire, c'est tout simplement les ENLEVER.
L'enseignant prit 10 blanches dans sa main.
P : Enlève 7 B.
L'élève, qui commençait à s'habituer aux questions simplistes de son enseignant s'exécuta.
E : Et hop là ! il reste 3 B.
P : Effectivement. Symboliquement on a (+10) - (+7) = (+3). C'est un peu enfantin...
E : Je suis bien d'accord avec vous.
P (En prenant 10 N dans sa main) : Ok. Enlève 3 pierres noires.
E (en exécutant la consigne) : Vraiment, y'a rien là. Attendez, je vais vous écrire ce que cela représente symboliquement. (-10) - (-3) = (-7). C'est bizarre, quand je vois l'opération dans ma tête (avec les pierres) il me semble que c'est vraiment une opération niaiseuse. Pourtant, juste avant d'entrer ici, j'y comprenais rien à la soustraction.
P : Attends ! On n'a pas terminé.
Puis, il prit 5 B dans sa main.
P : Enlève 2 pierres noires.
E : ???
P (insistant) : E N L È V E 2 pierres noires.
E : J'peux pas. Vous n'en avez pas dans votre main.
P (souriant) : Si, j'en ai
E (têtu) : Non, il n'y en a pas.
P (regardant l'élève droit dans les yeux) : Regarde comme il faut ! J'AI DES PIERRES NOIRES DANS MA MAIN.
L'élève, croyant que son professeur était en train de devenir fou, secoua la tête. Après quelques secondes, l'enseignant s'enfonça dans le dossier de sa chaise et lui dit :
P : Tu te rappelles au début de la leçon? Je t'avais dit que tu oublierais la définition des entiers. C'est justement ce que tu fais en ce moment. J'ai gagné mon pari.
Encore une fois, l'élève fronça les sourcils et ne comprenait pas ce qu'il se passait. L'enseignant ouvrit sa main qui contenait les 5 pierres blanches.
P : Regarde bien. Il y a dans cette main, une infinité de pierres noires. MAIS TU NE LES VOIS PAS. Elles sont pourtant bien là.
Puisque l'élève ne semblait pas trop saisir les propos de l'enseignant, ce dernier prit un couple de pierres b/n et les déposa dans sa main.
P : Es-tu d'accord pour dire que 5 B, c'est comme 6 B et 1 N, puisque selon la définition des entiers...
E (en coupant l'enseignant) : Ça y est. Je viens de comprendre. C'est comme si vous ajoutiez des zéros. Ce qui dans le fond, ne change rien...
P : C'est ça. On a ce qu'on pourrait appeler des états équivalents. Donc, peux-tu enlever 2 N à mes 5 B?
E (fier de lui) : Bien sûr !
Et il ajoutant aux 5 B deux couples de (B/N). Puis, il prit les 2N. Il restait 7B dans sa main.
E : Symboliquement on a : (+5) - (-2) = (+7). Hé, hé, facile !!!
P : En effet, c'est pas si compliqué que ça. Encore une fois, j'aimerais que tu fasses bien la distinction entre l'opération soustraction symbolisée par un moins. Et le moins qui représente les pierres noires.
E (content de son jeu de mots) : Oui,oui, je vois bien la différence.
P: Ok. Voyons comment tu vas résoudre celui-ci.
L'enseignant mit 5 pierres blanches dans sa main.
P: Enlève 8 pierres blanches.
E (ne trouvant pas le défi tellement difficile) : Bof ! Il suffit d'ajouter ... hum... trois couples B/N. Ainsi, je pourrai soustraire les 8 pierres blanches... Il me restera alors 3 pierres noires. Donc, (+5) - (+8) = (-3). C'est tout de même bizarre de voir apparaître des N alors qu'on enlève des B.
P : Oui. Je suis d'accord avec toi. Il y a comme un brin de magie là-dedans. Mais tout cela ne découle que de la définition, ou si tu veux, de la nature même des nombres entiers. Ils sont vraiment surprenants ! Bon, regarde ce problème.
Et l'enseignant, sur un bout de papier écrit : (-10) - (+1). D'après toi, qu'est-ce que cela donne?
E : Bon, j'ai 10 pierres noires. Je dois enlever une pierre blanche... Bien, il suffit que j'ajoute un seul couple B/N. Si j'enlève maintenant la pierre blanche, il me restera 11 N. Donc, la réponse est (-11).
En résolvant le problème, l'élève manipulait les pierres. C'est ainsi que l'enseignant posa encore quelques questions pour s'assurer que l'idée était bien entrée dans le cerveau de son élève. Puis, il lui demanda.
P : Que donne maintenant cette expression : (-142) - (+99)?
L'élève souriait. Les nombres étaient beaucoup plus gros mais il ne sentait plus la nécessité d'utiliser les pierres.
E : Hum... Je dois enlever les blanches, mais il n'y en a pas dans mes 142 N. Donc, je dois ajouter à ces 142N, 99 couples (B/N). Ainsi, en enlevant les 99 B, je me retrouve avec 99 N de plus, donc... 241 N. Ma réponse : (-241).
La cloche venait de sonner. L'enseignant était fier des progrès de l'élève.

Notes pédagogiques

1. Il faut s'assurer que la notion d'addition chez les naturels est très bien comprise par l'élève. Dans le texte, l'enseignant devrait sans doute appuyer sur le fait qu'on ne peut additionner que des natures semblables (des pommes, des oranges, des fruits.)
2. Le modèle pierre blanche, pierre noire est utile pour l'ensemble des opérations chez les entiers. Par exemple, pour la multiplication, voyez ce billet. Il peut aussi servir à la relation d'ordre. Il permet donc de garder une cohérence dans les explications. On voit souvent l'addition expliquée à partir d'une droite numérique ou comme des comptes bancaires avec un actif et un passif, etc. Pour la soustraction, on noie l'élève dans une règle (soustraire c'est additionner l'opposé!!!!) sortie du chapeau magique de l'enseignant.
3. Il est très important de conserver les parenthèses lorsqu'on initie les élèves aux nombres entiers. Quand on sera assuré que le concept est bien compris, on pourra lui suggérer de supprimer ces parenthèses.
4. Énoncer des règles du genre «si on additionne un entier positif avec un entier négatif, on doit soustraire le plus grand du plus petit et donner le signe du plus grand», c'est prendre l'élève pour un idiot. Il faut que l'élève COMPRENNE les opérations sur les entiers. L'élève qui aura compris le principe de l'addition se fera ses propres règles, s'il en sent le besoin.
5. Laissez tout le temps nécessaire aux élèves de manipuler les pierres. Il faut qu'ils sentent les opérations. Je suggère de toujours associer les manipulations à la représentation symbolique. Éventuellement cette seule représentation symbolique sera suffisante. Encore une fois : laissez le temps aux élèves de manipuler les pierres. Et je répète : laissez le temps aux élèves de manipuler les pierres.

Dans l'un des très nombreux commentaires au billet Défi à Découverte, M. Lyons demande comment faire pour expliquer le problème donné en titre à de jeunes enfants. Il nous donne aussi deux cas concrets de cet énoncé. Je reviens ici sur ces exemples, car, à mon avis, ils ne rendent pas vraiment justice à l'énoncé.

Exemple 1 : «[...] les postes d'essence vendront leur précieux liquide au demi-litre et que 1$ pour 1 demi-litre semblera moins dispendieux que 2$ du litre (ce qui se calcule en effectuant : 1$ ÷ ½ = 2$).»

En fait, la question ici est si ½ litre vaut 1 $, que vaut 1 litre?

Algébriquement, on a : Soit x la valeur d'un litre, alors ½x = 1$ (un demi litre vaut 1$). Évidemment, personne à part un prof de maths ou, comme moi, un ex-prof de maths, ne pensera à mettre ce problème en équation.

La solution est donc : x = 1$ ÷ ½ = 2$. Cependant, dans la tête de la majorité des gens, à mon avis, on ne resout pas du tout ce problème de cette manière. On fait plutôt :

2 · ½x = 2 · 1$ donc x = 2$. Ici, il n'y a eu AUCUNE division !!! Posez ce problème autour de vous et je suis à peu près convaincu qu'on vous répondra tous par «Ben voyons, ça va coûter 2 fois 1 $.» Il m'étonnerait grandement qu'un seul de vos répondants parle de DIVISION!

Exemple 2 : «[...] j'apporte seulement 20$, ce qui risque de ne représenter que la moitié du prix de ma commande (Je prévois que cette commande devrait coûter 20$ ÷ ½ = 40$).»

C'est le même problème que l'exemple 1, mais cette fois, on remplace le mot demi par moitié. Algébriquement : 20 $ = x/2 (la moitié de x). Encore une fois, je pense que toute personne non-mathématicienne le résout non pas en divisant 20 par ½, mais bien à multipliant 20 par 2. On arguera que cela revient au même. Mais je crois que pour appuyer sur la notion de division, on doit trouver des problèmes qui appellent d'abord ce concept dans sa résolution.

Les exemples cités ne sont pas, d'après moi, des exemples concrets de 1$ ÷ ½ mais plutôt la manière d'écrire une résolution d'une équation du premier degré de type ½x = 1. Didactiquement parlant, je crois que la question qui'il faut se poser est la suivante : peut-on expliquer l'opération division sans avoir besoin du concept de la multiplication? Autrement dit, peut-on illustrer la force de la division pour ce qu'elle vaut en elle-même?

Voyons chez les nombres naturels.

12 ÷ 4. On s'entend généralement sur deux interprétations ici :

1. La division contenance : Combien de paquets de 4 pommes peut-on faire avec 12 pommes. Il faut apprendre à l'enfant que le symbole ÷ est bien pratique pour illustrer l'idée de contenance. Remarquez aussi que les unités du dividende et du diviseur sont les mêmes. La réponse est un nombre de paquets.

2. La division partage : Prenons un cas classique. On achète un cadeau de 100$ à un ami et on se partage le coût à 8 personnes. La solution arithmétique appelle clairement une division. On ne pensera généralement pas «8 fois quoi donne 100$», mais plutôt «100 divisé par 8 donne le montant que je dois payer.» La réponse est un coût par personne. À mon avis, ce genre de problème fait partie de l'univers de la division.

La beauté de la division chez les naturels est qu'elle peut se percevoir facilement comme une opération à part entière et qui n'a pas vraiment besoin de l'opération multiplication pour exister, car la symbolique de la division représente ces idées de partage ou de contenance.

C'est seulement par la suite qu'un enfant pourra «découvrir» que la division et la multiplication sont deux visions d'une même réalité conceptuelle, mais avec de jolies exceptions (par exemple 8x0 = 0, mais 0÷0...) C'est un peu comme cette illusion d'optique où on voit parfois une vielle dame, parfois une jeune fille. L'enfant apprendra à «voir» une division dans la multiplication et une multiplication dans la division.

Peut-on illustrer purement (c'est-à-dire sans avoir à l'esprit l'opération inverse de multiplication) la division de fractions? Y'a-t-il des situations vraiment concrètes, comme celle du prix du cadeau qu'on se partage) qui force naturellement l'utilisation de la division par une fraction? En cinquante ans, dans ma vie de tous les jours, je n'ai jamais rencontré ce genre de problèmes... Même si j'en avais rencontré une ou deux fois, cela mérite-t-il qu'on s'y attarde à l'école? Si oui, pourquoi? (Ma réponse, qui est positive, fera sans doute l'objet d'un futur billet. En attendant, pourquoi ne pas m'indiquer la vôtre?)

Par ailleurs, je crois qu'il est judicieux d'imprégner les enfants dans le langage «fractionnaire» (moitié, demi, tiers, etc.) et je crois qu'il réussira à peu près sans peine à trouver plein de réponses à des questions du genre «Papa te donne 5$ mais ça correspond à la moitié du jeu que tu veux acheter. Combien coûte le jeu?» Mais il m'étonnerait grandement qu'il fasse dans sa tête l'opération division pour résoudre ce problème. Comme la majorité d'entre nous, il multipliera simplement pas deux.

Cela me rappelle le texte ci-dessous que vous trouverez dans le merveilleux petit livre de Normand Baillargeon publié chez Lux «Petit cours d'autodéfense intellectuelle».

«On vous montre, déposée sur une talbe, quatre cartes dont les faces visibles indiquent :
D - F - 3 - 7
Chaque carte présente sur une face une lettre et sur l'autre face un chiffre. On vous demande ensuite quelles cartes vous devrez retrouner pour vérifier que la règle suivante a été respectée : si une carte présente un D sur une face, alors elle doit avoir un 3 sur son autre face.
L'expérience, qui a fréquemment été réalisée et avec un grand nombre de sujets, montre qu'à moins d'avoir fait des mathématiques un peu avancées, de la logique ou de la programmation, la plupart des gens répondent D et 3, soit la première et la troisième carte. Ce n'est pas exact : il faut retourner la première et la dernière carte.
La premère parce qu'il pourrait y avoir autre chose qu'un 3 sur l'autre face, ce qui infirmerait l'hypothèse. [...] De même, c'est pour confirmer l'hypothèse qu'on a retourné la troisième carte (le 3) : on cherchait un D de l'autre côté. Mais pensez-y: cela ne changerait rien quoi qu'il y ait de l'autre côté. L'hypothèse dit que s'il y a un D, alors il y a un 3; elle ne dit pas que s'il y a un3, il doit y avoir un D!
La quatrième carte est cruciale. S'il devait y avoir un D sur l'autre face, notre hypothèse serait réfutée. [...]
Ce petit test amusant a été repris par des chercheurs en psychologie évolutionniste pour montrer que, si l'on raisonne sur un exemple mettant en jeu la détec­tion de tricheurs, le raisonnement devient beaucoup plus facile. Voyons de quoi il retourne pour conclure sur ce sujet.
On vous explique que vous travaillez comme res­ponsable de la sécurité dans un bar. Ce bar est acces­sible à des jeunes de moins de 18 ans et à des adultes. Cependant, les jeunes gens ne doivent absolument pas consommer d'alcool. Si un jeune de moins de 18 ans était surpris à en consommer dans le bar, celui-ci perdrait aussitôt son permis. Votre tâche, en tant que responsable de la sécurité du bar, est de vous assu­rer qu'aucun jeune n'y consomme d'alcool. Heureu­sement, chaque client circule en portant, bien visible, une carte : sur une des faces on trouve un chiffre, qui indique son âge; sur l'autre face, ce qu'il consomme.
Vous êtes dans le bar et vous remarquez les quatre cartes suivantes
Cola Bière 28 16
Quelles cartes retournerez-vous pour vous assurer que personne ne consomme d'alcool illégalement?
Notez que, bien qu'il soit facile et résolu par tout le monde, sur le plan formel, ce problème est exacte­ment le même que le précédent. » (pages 208-209)

Il est rare qu'on entende parler des mathématiques au primaire à la télé. Dimanche dernier, on a eu droit à un petit 15 minutes avec M. Robert Lyons. Ce dernier a illustré que les enfants étaient capables de factoriser des trinômes. Je reviens sur ce problème car il cache selon moi d'énormes pièges. Comme on ne voyait pas la fin de la leçon de M. Lyons, il est difficile de porter un jugement sur l'efficacité de celle-ci.
Les enfants devaient factoriser 6x² + 5xy + y².

Au tableau, on voyait 6 carrés, 5 bâtonnets et un petit cube. L'enseignant demandait aux élèves de faire un «plancher» rectangulaire et sans trou avec ces formes. (Désolé pour mon illustration : j'ai fait ça rapidement avec OpenOffice Draw.)

Après quelques essais, tous arrivaient à un résultat pouvant se traduire par «la réponse» (3x + y)(2x + y).

Clairement, le carré représentait le x·x. Le bâtonnet : x·y et M. Lyons avait choisi le cube comme représentant y². Mais le plus dangereux est que cette représentation est ... incohérente : Pourquoi un cube pour représenter un carré ??? Je n'ai entendu aucun enfant poser la question. Il est vrai que pour la durée du reportage, ils ont certainement dû couper plusieurs interventions des élèves ce qui est bien dommage. En tout cas, j'aurais bien aimé entendre la réponse de M. Lyons.

Autre question. Pourquoi prendre un carré (physique) pour représenter x² ? Tout le monde répondra par l'évidence même que x·x PEUT être représenté par un carré. Ah oui? En fait, un NOMBRE naturel carré peut être FIGURÉ (on appelle d'ailleurs cela un nombre figuré) sous une forme carrée. Par exemple, 16 est un nombre carré.

Il y aussi des nombres triangulaires (1, 3, 6, 10, etc.), pentagonaux, etc. desquels on peut trouver d'intéressantes propriétés.

Clairement on peut représenter x² sous la forme d'un carré si on sait que x fait partie de l'ensemble des réels positifs non transcendants (par exemple pi² ne peut pas se réprésenter sous forme d'un carré de pi sur pi car pi est transcendant.). Or, pour bien faire les choses, l'algèbre étant d'abord une généralisation utile, dans le trinôme de départ, x et y sont des nombres RÉELS (généralisation utile) et, donc, peuvent être entre autres négatifs ou transcendants. Quel sens aura alors ce carré physique si x est négatif? Et la factorisation est-elle toujours possible dans les cas où x ou y sont transcendants? L'image mentale d'un carré risque ici de nous amener une conclusion qui pourrait être fausse pour TOUS les nombres. D'accord, ce n'est pas le cas ici, mais il reste que cette image ne peut être utilisée comme preuve. Cette vision donne de la plausibilité à la réponse mais n'est en aucun point algébriquement et mathématiquement rigoureuse. La manipulation peut servir de support au raisonnement, mais elle ne le remplace pas. Encore une fois, le reportage ne montrait nulle part les questionnements soulevés par les élèves. L'objectivation était aussi absente du montage.

Par ailleurs, la traduction d'un nombre carré en surface peut aussi poser problème. 16 peut prendre la forme d'un carré, mais on ne parlera certainement pas ici de surface ! Or, le plancher, c'est d'abord une surface. Mais j'ai déjà parlé de ce piège dans un autre billet.

L'idée de factoriser «physiquement» est riche et vraiment intéressante. On voit la solution apparaître sous nos yeux et on a l'impression que l'algèbre, c'est pas si compliqué après tout. Mais pour ne pas créer de fausses représentations dans l'esprit des élèves, il faut porter énormément attention sur ce que les enfants ont réellement compris. Et s'assurer que malgré la simplicité de l'algèbre, l'élève sache bien que ce n'est tout de même pas une matière simpliste.

Un matin, juste au lever du soleil, un moine bouddhiste commence à gravir une montagne. Le sentier, très étroit, monte en spirale jusqu'au temple qui brille au sommet.
Le moine grimpe tantôt vite, tantôt lentement et s'arrête plusieurs fois pour se reposer et manger les fruits secs qu'il tire de sa besace. Il arrive au temple peu avant le coucher du soleil. Après quelques jours de jeûne et de méditation il se met en devoir de redescendre, part au lever du jour, prend le même chemin, va plus ou moins vite, s'arrête plusieurs fois. Cependant il va plus vite en moyenne, bien entendu, à la descente qu'à la montée.
Démontrez qu'il existe un point du sentier que le moine occupera à chaque voyage exactement à la même heure.

(Scientific American, 1961. J'emprunte ici la version tirée du livre Le cri d'Archimède, d'Arthur Koestler, Calman-Lévy, 1965, trad. Geroges Pradier.)

Écoutons Koestler : « Je me suis amusé à poser ce problème à des amis, hommes de science et autres. Certains essayent les mathématiques; certains veulent "raisonner" et arrivent à la conclusion que ce serait une coîncidence invraisemblable que le moine se trouve à la même heure au même endroit en deux occasions différentes. Mais d'autres - appartenant à la catégorie des visuels - voient la solution [...].» (op. cit. p. 166)

Voyez-vous la solution?

Pour ceux qui seraient tentés d'utiliser les mathématiques, voici le théorème qui vous aidera :

Lu dans Vie & Santé, août 2005, p.52 (c'est moi qui souligne) :

« Chez 5% à 10% des enfants d'âge scolaire, la capacité de lire se situe sous la moyenne. » (Raynald Bouchard)

J'ai eu l'occasion de feuilleter un manuel scolaire de sience de première secondaire en fin de semaine. Dans ce dernier, au chapitre sur la cellule, un encadré mathématique (il faut bien faire des liens, n'est-ce pas?) dans lequel on signale que les mathématiques sont bien utiles pour écrire de grands nombres. Et le tableau suivant est affiché, sans plus de détails:

10⁰ = 1;
10¹ = 10;
10² = 100;
10³ = 1000;
10⁴ = 10000;
10⁵ = 100000;
10⁶ = 1000000;
10⁷ = 10000000;
10⁸ = 100000000;
10⁹ = 1000000000;
10¹⁰ = 10000000000;
etc.

Ce qui me chicote, dans ce tableau, est l'explication que peut en donner un enseignant pour signaler que 10⁰ donne 1.

Explication poche nº 1

-Tu vois l'exposant? Il représente le nombre de zéros. Dans 100 il y a deux zéros, dans 1000, trois zéros. L'exposant correspond donc au nombre de zéros. Il est donc normal que 10⁰ donne 1, puisqu'il n'y a pas de zéro.

Cette explication est vraiment poche. Quand l'enfant verra quelque chose comme 2¹⁰, il écrira peut-être 200000000. Un enfant essaie d'être logique. C'est souvent la mathématique scolaire qui lui enseigne la magie car l'enseignant, avec de gros yeux, le reprendra en lui disant qu'il est tout faux et que 2¹⁰ vaut 1024 

Explication poche nº 2

- Prends une ligne du tableau. Si tu remontes, tu dois diviser par 10. Si tu descends, tu dois multiplier par 10. Par exemple, à partir de 10² = 100, si tu divises par 10, tu obtiens 10¹=10 et si tu redivises encore par 10 tu obtiens 10⁰=1. Logique, non?

Logique? Pas du tout. Car, voyez-vous, pour réaliser cette opération de remonter ou de descendre, il faut être à quelque part ! Or, comment déterminer que, par exemple, 10⁵ = 100000 ? L'enseignant pourra dire que l'exposant est le nombre de zéros. Mais là, on retombe dans l'explication poche nº 1.

Il sera donc obligé de dire que 10⁵, c'est tout simplement 10 qui s'est multiplié cinq fois par lui-même.

- Mais alors, demandera l'élève, comment se fait-il que 10 multiplié zéro fois par lui-même donne 1???

Expérons que le prof ne cafouillera pas trop dans son explication.

À mon avis, il aurait été bienvenu que le tableau ne contienne pas la ligne 10⁰ = 1. Car l'explication du nombre multiplié tant de fois par lui-même est correcte : l'enfant trouvera alors cohérent que 2¹⁰ donne 1024, car c'est 2 multiplié 10 fois par lui-même ! Pour aller plus loin (les exposants 0, négatifs et fractionnaires), il aurait été intéressant que l'enseignant de science qui désire aborder la notation des grands nombres et la notation scientifique, coordonne cette explication avec l'enseignant du cours de maths. Dans le manuel, on aurait pu écrire quelque chose du genre : « Tu veux savoir quel sens peut avoir par exemple 10⁰ ou 10^-4 ou 10^3/5 ? Demande à ton enseignant de mathématiques ! Ton enseignant de science t'indiquera que ces exposants bizarres sont très importants dans plusieurs domaines scientifiques ! »

Un extrait d'une entrevue de Denis Guedj :

CS : Les maths ont mauvaise réputation. Pourquoi ?
D. G. : Il y en a qui n’aiment pas le caviar sans savoir ce que c’est, et d’autres qui, connaissant le caviar, ne l’aiment pas non plus. C’est la même chose pour les mathématiques. Ça met en jeu un certain nombre de choses, comme la rigueur et la démonstration. Certaines personnes y sont hostiles. Elles n’aiment pas ça et elles ont le droit de ne pas aimer ça ! Ça ne sert à rien de les culpabiliser.
Il faut dire aussi que le statut de l’enseignement des mathématiques aujourd’hui est particulier. Avec le français, les mathématiques sont considérées comme la matière la plus importante. On peut comprendre que l’on accorde beaucoup d’importance à l’enseignement de la langue maternelle. Les maths, par contre, sont beaucoup moins proches de la vie quotidienne. D’une certaine façon, elles sont même devenues un outil de coercition : si on n’est pas bon en maths, on va avoir des ennuis, on n’aura pas une bonne scolarité, etc. Conséquence : on a peur et on ne comprend pas. Et plus on a peur, moins on comprend. Mais contrairement au sport, on ne peut pas obtenir de certificat médical pour ne pas faire de maths...

CS : Y aurait-il trop de maths à l’école ?
D. G. : En France, on fait des mathématiques durant toutes ses études. Jusqu’au baccalauréat, ça fait plus de 12 ans. Elles ne devraient pas être obligatoire si longtemps. Ou on devrait changer la manière de les faire. Apprendre à résoudre des équations du second degré, est-ce vraiment si important ? D’une certaine manière, ça ne sert à rien - au sens où les gens disent servir - mais ça peut être utile à énormément de choses : qu’est-ce que c’est qu’une équation ? Qu’est-ce que c’est que ces inconnues, les petits « x », les petits « a » ? On va trop vite sur l’apprentissage de ces notions, alors que c’est très dur à comprendre.
Au lieu de mettre l’importance sur l’accumulation des connaissances, on devrait passer plus de temps sur les mécanismes des mathématiques, comme la logique, la rigueur, etc. Qu’est-ce qu’un raisonnement par l’absurde, par exemple ? Contrairement à ce que l’on enseigne habituellement, on peut partir d’une hypothèse fausse pour arriver à démontrer que quelque chose est vrai.
Il faudrait inculquer une culture mathématique plutôt que faire des maths. La culture mathématique, ce serait lire ou écrire les maths. Je t’écris des maths et tu me dis qu’est-ce que ça dit. C’est important, parce que le moment de l’écriture est absolument nécessaire. Vous pouvez faire de l’histoire ou de la géographie sans écrire, mais vous ne pouvez pas faire de mathématiques sans écrire - ou du moins dans les maths de notre culture grecque. Il faudrait également enseigner l’histoire des mathématiques. Ça cultiverait les gens, mais surtout ça les aiderait à mieux comprendre les maths.

Voir le Blog-notes du Coyote.

Dans l'excellent Challenging Problems in Geometry de Posamentier et Salkind (Dover, 1996), les auteurs comparent la méthode du paysan et la méthode du poète en matière de résolution de problèmes (peasant's way, poet's way). Pour comprendre ces deux approches, ils donnent un problème semblable à celui-ci :

Trouvez la somme des inverses des nombres dont la somme est 7 et le produit est 8.

Pour ceux d'entre vous qui ne sont pas du tout matheux, je vous prierais de continuer tout de même la lecture, quitte à sauter les côtés trop mathématiques de la solution. En effet, mon but n'est pas ici de faire des maths, mais de vous faire plutôt ressentir une belle solution, même si les connaissances exigeant cette résolution vous font défaut. Et puis, à la toute fin du billet, vous pourrez tenter un petit problème beaucoup plus simple et dont la solution n'exige aucune habileté mathématique. Ce problème illustrera un autre exemple de la paysannerie versus la poésie.

D'abord, pour bien comprendre le problème énoncé ci-haut, je rappelle que l'inverse d'un nombre x est 1/x. Par exemple, l'inverse de 4 est 1/4 ou 0,25.

La manière paysanne (et telle fut d'ailleurs mon approche !) de faire les choses est la suivante :

Posons le système d'équations
x + y = 7
et
xy = 8

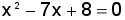Par simple substitution, cela revient à résoudre l'équation du second degré : . De là, on trouve facilement x et, par la suite y. Il suffit ensuite d'additionner l'inverse de ces nombres. (Ici, 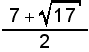et 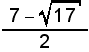sont les deux nombres.) La somme des inverses de ces nombres donne 7/8, qui est la réponse cherchée. Si vous faites correctement toutes les étapes, elles peuvent facilement vous demander une quinzaine de minutes de concentration.

Voyez maintenant la méthode dite du poète :

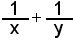On cherche . Or, algébriquement parlant, si on fait l'addition, on a 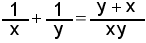. Et, sans connaître x ni y, on sait que cela correspond à 7/8, car la somme (7 dans la donnée du problème) est au numérateur et le produit (8 dans la donnée du problème) est au dénominateur ! La réponse est trouvée en quelques secondes, et, ma foi, d'une manière fort élégante. Autrement dit, la solution ne passait pas nécessairement par la découverte des deux nombres en question.

Voyez maintenant ce petit problème très cher à mon collègue philosophe Mario :

120 élèves se présentent à un tournoi scolaire de ping-pong. Seuls des matchs simples sont disputés. À chaque match, l'élève perdant est éliminé et le vainqueur continue jusqu’à ce qu’il ne reste plus qu’un seul grand gagnant. Combien de parties seront jouées ?

Pensez-y quelques minutes. Puis, regardez les deux solutions ci-dessous:

(Paesant's way) :
Ronde 1 : 60 parties
Ronde 2 : 30 parties
Ronde 3 : 15 parties
Ronde 4 : 7 parties (reste un joueur qui a un bye)
Ronde 5 : 4 parties.
Ronde 6 : 2 parties.
Ronde 7 : 1 partie.
Donc, on doit disputer 119 parties.

(Poet's way)
Une partie élimine un joueur. Il faut éliminer 119 joueurs. Donc 119 parties seront nécessaires !!!

Pour finir

En ce qui concerne le premier problème, la méthode paysanne exige une bonne technique mathématique. Si vous avez réussi dans votre vie un cours de niveau 4^e secondaire, vous avez tous les outils pour le résoudre de cette manière. Cependant, je suis à peu près convaincu que même si vous avez réussi ce cours avec une très bonne note, vous avez sans doute bloqué à un moment ou à un autre. Pourquoi ? Tout simplement parce que les techniques enseignées au secondaire non seulement s'oublient, mais elles sont à peu près complètement inutiles au commun des mortels. Or, vous en avez probablement fait des tonnes de problèmes tels celui des deux nombres. Tout ce qu'on a sans doute réussi à faire avec ces exercices, c'est de vous donner une bonne écoeurite des mathématiques. C'est pourquoi je milite pour un arrêt de l'enseignement des maths au secondaire. J'irais même jusqu'à dire que cet enseignement nuit à l'essor de la pensée logico-mathématique chez les enfants. D'après moi, l'école crée beaucoup plus de mathophobes que de logicophiles! Il est vrai que la solution du poète demande aussi une connaissance mathématique (addition de fractions algébriques.) En fait, la beauté ici ne réside pas du tout dans la question qui est, scolairement parlant, assez banale, mais plutôt dans le HAHA de sa solution poétique. Certains qui aiment les maths aiment aussi ces twists intellectuels.

Petite question : Qu'arriverait-il si je donnais le premier problème à résoudre à des enseignants du primaire? Je vous laisse deviner les réactions. Ne serait-ce point là une belle manière d'aborder les émotions en maths !