Jobineries

Hier, dans une classe de quatrième année, j'ai pu observer la puissance de ces objets-pour-penser-avec.¹

Le jeune Alex, qui avait environ 2 heures de Scratch dans le corps, était dans son projet. Fond d'écran, la mer; deux objets : un bateau et le chat dans le bateau.

- Je veux que mon chat tombe à l'eau.
- Oh, c'est violent.
- (Sourire d'Alex). Mais je sais pas comment faire.
- Où veux-tu qu'il tombe ?
Alex pointe l'endroit à l'écran.
- Hum... T'as appris le plan cartésien ?
À l'expression du jeune, j'avais ma réponse.
- Ok, c'est pas grave. Mets ta souris exactement où tu veux que ton objet tombe. Tu vois les deux nombres dans le coin de l'écran ? (Il les lit, lentement). Il faut que tu t'en souviennes. C'est la manière de dire à l'ordinateur que « c'est là ».
- Bon, mais je fais quoi avec ces nombres ?
- Tu n'as qu'à dire à l'objet de s'y rendre.
- Mais, Monsieur Gilles, je sais pas comment faire ça.
- Il y a une jolie brique qui vient à ta rescousse. À côté du x, tu poses ton premier nombre, et à côté du y, le second.
Il s'exécute et me lance un Ahhhhhhhh ! Puis, froncement de sourcils.
- Et si je veux qu'il bouge ailleurs après, je fais comment ?
- Tu fais la même chose... Essaie, et si tu as de la difficulté, rappelle-moi.

Plusieurs minutes après, je suis repassé dans son coin de la classe. Il avait réussi à contaminer plusieurs de ses camarades avec cette brique « glisser ». Tous ces élèves utilisaient d'une manière tout à fait naturelle et intuitive les coordonnées cartésiennes. Maîtrisaient-ils la notion ? Certainement pas. Mais peut-on demander à un petit québécois qui arriverait en Italie de maîtriser immédiatement l'italien ? L'amener dans un restaurant, et le laisser se débrouiller un peu pour demander un verre de lait n'est-il pas un bon début pour apprendre la langue ? Alors pourquoi demander à un élève qui arrive en Mathématie de maîtriser une notion mathématique avant de l'utiliser ?

[1] Voir Papert et son Jaillissement de l'esprit.

Martin Gardner, né en 1914, est quant à moi l'un des cinq plus grands généralistes^[1] du XX^e siècle.

Je cherchais sur Amazon s'il n'avait pas récemment publié. J'ai en effet une trentaine de ses livres, dont tous ses recueils de récréations mathématiques du Scientific American, et j'aime bien les écrits de ces hommes qui ont encore toute leur tête alors qu'ils approchent le centenaire.^[2]

C'est ainsi que je suis tombé sur le CD-ROM contenant les quinze recueils en PDF acceptant la recherche. Évidemment, je n'ai pu résister...
C'est grâce à Gardner si je me suis intéressé aux automates cellulaires et au jeu de la vie de Conway, aux polyominos de S. W. Golomb, au jeu de Nim, à Sam Loyd, à Lewis Carroll, à l'OULIPO, au jeu Eleusis, aux épigraphes - car il en mettait souvent au début de ses articles - et à tant d'autres choses encore.

Plus important, Gardner m'a permis de réaliser que les mathématiques scolaires sont un reflet terne de la culture mathématique.

MàJ (quelques heures après publication) : Sur l'excellent Blog à Maths, un billet annonçant la brochure gratuite Maths Énigmes Express. Le dernier chapitre est consacré à Gardner. À lire !

[1] Je mettrais aussi dans cette catégorie Edgar Morin, Michel Serres et Bertrand Russell.
[2] Henry Bauchau est un autre exemple.

Mathématiques et sentiments, un billet écrit le 5 mars dernier par Fabien Besnard du blogue Mathéphysique m'a fait grand bien ce matin.

Hier après-midi, l'émission de France Inter La tête au carré avait pour sujet principal «À quoi servent les mathématiques ?» avec Benoit Rittaud et Denis Guedj comme invités.

Vous avez quelques jours seulement pour écouter l'émission archivée.

J'ai été assez décu, m'attendant à avoir au moins quelques réponses. Il s'agissait, semble-t-il, plutôt de ploguer les récents livres des mathématiciens.

Cela a tourné un peu autour de l'école, avec un Guedj plutôt hésitant, et un Rittaud plutôt réservé. Idem pour la distinction garçons-filles, les invités ne voulant pas s'engager dans une polémique. Bref, une entrevue qui manquait de punch. Mais certaines interventions dans les commentaires sur le site valent cependant la peine.

Trois idées que j'ai retenues : 1. Les théorèmes racontent une histoire; 2. Très vite une personne va parler d'elle lorsqu'on initie une conversation autour de la mathématique. 3. Les maths n'ont pas la cote médiatique. Après le parcours scolaire, on n'en entend plus parler. Donc, pour la grande majorité de la population, les mathématiques, ce sont d'abord les mathématiques dites scolaires.

Sur le site M@ths et tiques, on trouve, entre autres belles choses, des fonds d'écran mathématiques.

Jolie surprise qui m'attendait aujourd'hui au bureau.


En page 16, on trouve ces belles preuves sans mots.



La revue n'est pas encore disponible sur le site, mais cela ne saurait sans doute tarder.

La géométrie plane exerce sur moi une profonde fascination. Depuis l'apparition des mathématiques dites modernes en pédagogie (fin des années 60), les programmes ont laissé tomber une grande part de la géométrie plane classique (axiomes, prépositions, théorèmes, preuves...) pour la remplacer par des bidules plus utilitaires du genre description de solides ou de figures planes, application de certains théorèmes, etc.

Pourtant, l'un des très grands intérêts de la géométrie réside dans la créativité exigée pour démontrer des théorèmes. Il me semble aussi qu'on peut goûter à la beauté intellectuelle en visionnant certains résultats. Voyez par exemple cette illustration du théorème de Thébault, découvert en 1937.

Sur les côtés d'un parallélogramme, on construit des carrés. Le théorème dit que si, à partir des centres de ces carrés, on construit un polygone alors ce polygone sera aussi un carré !


Dans la figure, vous pouvez déplacer les points A, B et C pour vous persuader de la validité du théorème. La molette de votre souris agrandit ou rétrécit l'image.

Il reste bien sûr à le démonter rigoureusement. Mais je m'intéresse plutôt à l'émotion engendrée par le théorème. Trouvez-vous ce théorème BEAU? Vous laisse-t-il indifférent? Dans l'un comme dans l'autre cas, comment expliquer les sentiments ressentis? Comment se fait-il que certaines personnes soient atteintes par un tel résultat, alors que d'autres n'y voient que de la bouillie pour les chats ou une incommensurable perte de temps?

La situation est semblable en art. Comment se fait-il que certains soient charmés par une fugue de Bach, alors que d'autres s'ennuient à son écoute? qu'un poème de Nelligan nous laisse insensibles alors que d'autres en pleurent d'émotion?

Je n'ai pas de réponse, et il me semble que s'il y en avait une, elle me décevrait. Car j'aime bien cette différence. Cela me rappelle que l'autre est un mystère, non pas une machine bien programmée. La beauté se trouve dans à peu près tout. Au cerveau de décider. « Que l'importance soit dans ton regard, non dans la chose regardée », disait Gide. Et n'est-ce pas là notre rôle, comme parents ou pédagogues, de reconnaître la flamme dans le regard d'un enfant?

-Wow, c'est don' ben' beau!

J'étais dans une classe de primaire, deuxième cycle. Je m'apprêtais à une petite séance Squeak, mais des enfants lançaient les exclamations devant mon fond d'écran.

- Vous savez ce que c'est ?

- Un bonhomme pain d'épice ?

- Non.

- Un trou noir ?

- Mais non !

- ...

- C'est un objet fractal.

- ...

- Vous savez ce qu'est une dimension ?

- (La titulaire de la classe) Pensez à vos solides. Largeur...

- (Moi) Oui, oui, il y a la largeur, la hauteur, la longueur. La plupart des gens pensent qu'il y a trois dimensions. Mais depuis Einstein, on décrit généralement l'univers avec une quatrième dimension : le temps. Mais il y aussi un monsieur qui a découvert que certains objets avaient des dimensions bizarres, genre quelque chose entre 1 et 2. Ce sont ses objets qu'on nomme FRACTALS. Et on peut en donner une idée assez vague avec un ordinateur. L'image que vous voyez est l'une de ses idées.

- Ça l'air compliqué...

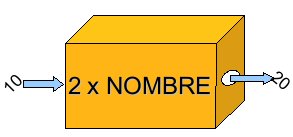
- (Moi, souriant) Oui et non. Attendez, je vais essayer de vous décrire un peu comment ça marche. Imaginez une boîte. Dans cette boîte, il y a une petite formule mathématique. On appelle ça une fonction. Il y a deux trous. Par l'un des trous, on entre des nombres, et ils ressortent par l'autre. Ici, par exemple, dans la boîte, il y a 2 fois nombre. Ça veut juste dire que si j'entre un nombre, il sortira multiplié par deux.

- Si j'entre 10, qu'elle sera la sortie ?

Tout le monde lance 20.

- Ok, si j'entre 100 ?

- 200!

- Bon vous avez compris. Mais la manière de construire un object fractal du type que vous voyez sur mon écran est basée sur le principe suivant. Quand j'entre un nombre, je regarde ce qu'il en sort, Et le nombre qui sort, je le "ré-entre" dans la boîte. Puis, je regarde ce qu'il en sort, et je ré-entre le nouveau résultat. Et ainsi de suite. Évidemment, un ordinateur fait ça très rapidement.

- (Un petit futé) Mais monsieur Gilles, les nombres doivent devenir très gros...

- Tu as raison. Par exemple ici, en commençant avec 10, j'aurai : 10, 20, 40, 80, 160, 320, 640, etc.

- Mais comment ça peut donner une image comme sur votre écran?

- C'est là que les choses deviennent intéressantes. L'idée est de vérifier à chaque fois le nombre qui sort. S'il dépasse une certaine valeur, on met un point d'une certaine couleur à l'écran selon le temps que cela lui a pris pour atteindre la valeur en question. Dans l'exemple que je vous donne ici, supposons que la certaine valeur est 100. C'est, disons, la limite que je m'impose. Si on commence par entrer 1 dans la boîte, on aura successivement :

2, 4, 8, 16, 32, 64, 128 (oups, après 7 itérations, on dépasse 100).

Si on entre par exemple, 15, on aura : 30, 60, 120, et trois itérations seulement ont été nécessaires.

Et là, la personne qui veut voir l'objet pourrait par exemple décréter que tous les nombres qui dépassent 100 après une itération sont noirs, après deux itérations sont rouges, après trois itérations sont bleus, etc. Dans certains cas, selon la formule qu'on met dans la boîte et des nombres qu'on y entre à tour de rôle, ça donne des trucs comme vous voyez sur mon écran.

- Monsieur Gilles ?

Une main est levée.

- Oui, Nicolas.

- C'est quoi la vraie formule qui donne votre dessin à l'écran?

Comment répondre à une telle question? Autant y aller avec la vérité. Et j'écris au tableau :

z² + c

zède, c'est le nombre que j'entre dans la boîte. z², ça veut juste dire que je dois le multiplier par lui-même. Par exemple, si mon z est 10, z² signifie que je dois faire z fois z, donc 10 fois 10 ce qui donne 100.

- Et le petit c, c'est quoi?

Il en pose des questions cet enfant...

- Le petit c, on appelle ça une constante. Ça veut juste dire que c'est un nombre qui ne change pas. Par exemple, supposons que c vaut 50. Alors on a z² + 50. Donc, si j'entre 10 dans la boîte, j'aurai : 10 fois 10, ce qui donne 100, et 100 + 50 donne 150. Il va donc falloir que je ré-entre dans la boîte 150. Ce qui va donner : 150 fois 150.... 22500 et si j'ajoute le 50, on a 22550...

- C'est gros...

- Oui, mais on peut entrer des nombres assez petits pour commencer. Car voyez-vous, il y a toutes sortes de nombres! Mais ce sera pour une autre fois...

J'utilise beaucoup le service de recherche de livres de Google. Je me sens comme à la bibliothèque, feuilletant de vieux grimoires.

Aujourd'hui, dans l'allée des mathématiques, j'ai trouvé beaucoup sur Euclide.

Par exemple, les Éléments par Déchalles et Ozanam (1778). Petit extrait :



Et là, tout à côté, Les élémenst d'Euclide expliqués.



Ou encore ce Peyrard, qui date de 1804.



Et comme j'admire Pierre de Fermat, voilà que je tombe sur son Varia Opera Mathematica publié en 1679 par son fils.



Évidemment, il faut être à l'aise en latin.

Dans le coin des curiosités mathématiques, j'ai feuilleté le Traité complet des carrés magiques, pairs et impairs de Violle.

Et puis, j'ai trouvé au moins trois versions du Legendre : Éléments de Géométrie de A.-M. Legendre. Et ici, la quatorzième édition, 1832. Et encore là, ce même livre, mais daté de 1843.

Lors d'une rencontre régionale, Charles Antoine a mentionné l'application web Wiris, une plateforme pour l'enseignement des maths. C'est en Java. Tout à fait extraordinaire ! À mettre de toute urgence entre les mains des enseignants et des élèves.

En essayant de comprendre comment créer des exercices dans CaRMetal, j'ai pondu celui-ci qui est, ma foi, très très simple.

Il faut construire, à l'aide des outils donnés, le centre du cercle. Il est en orange dans la figure. En réussissant, un beau bravo sera affiché à l'écran. Super, non?

Si votre géométrie est un peu loin, sachez que la médiatrice d'une corde passe toujours par le centre du cercle.

Depuis quelques semaines, j'explore quelques logiciels de géométrie dynamique. J'ai toujours admiré Cybergéomètre (Geometer's Sketchpad) à cause de son très grand potentiel comme aide au développement de scénarios d'apprentissage. Mais n'étant pas libre, je m'en suis détourné. Pour les linuxiens, sachez que GSP fonctionne très bien sous Wine.

Il y a quelques années, j'avais jeté un oeil sur C.a.R (Compas and Ruler) de l'allemand René Grothmann. Je viens tout juste d'y retourner, et j'avoue que la dernière version est absolument renversante. Vous n'avez qu'à passer au travers les différentes démonstrations en ligne pour vous en convaincre. Eric Hakenholz a développé une nouvelle interface (CarMetal) qui mérite le détour.

Il faut aussi visiter CARzine, un excellent site francophone consacré à C.a.R où vous trouverez de bons tutoriels.

J'ai fait rapidement un petit fichier pour voir si l'applet s'intègre bien à Dotclear. Et, comme vous pouvez le constater, c'est bien le cas. Vous pouvez donc vous attendre à quelques billets sur mes trouvailles dans les prochains mois.

En attendant, amusez-vous à déplacer le foyer ou la directrice. Je vous rappelle que la parabole est le lieu géométrique des points équidistants à une droite (la directrice) et un point (le foyer). Notez aussi que la distance d'un point à une droite est donnée par le plus court chemin de l'un à l'autre (la perpendiculaire issue du point à la droite.) Vous pouvez aussi zoomer à l'aide de la roulette de la souris.