mercredi 5 mai 2010
Les contresens
Par Gilles Jobin, mercredi 5 mai 2010 :: Mathématiqueries
Une foule d'absurdités encombre certains livres primaires. La théorie de la multiplication et de la division sont de pures calembredaines inintelligibles pour des enfants de moins de treize ans. Que de problèmes stupides sur les partages inversement proportionnels, sur des robinets dont l'un remplit et l'autre vide un réservoir !
Jules Payot, La faillite de l'enseignement, p.230, Librairie Félix Alcan, 1937.
Je relis beaucoup; je crois comprendre beaucoup mieux. C'est une vieillesse qui n'est pas sans charme que celle que l'on consacre à corriger ses vieux contresens.
Émile Faguet, L'art de lire, éd Armand Colin, p. 140.
Il n'y a pas de troubles mathématiques. Il n'y a que des enfants troublés.
Stella Baruk, Échec et maths, Éd. Seuil Points/S11.
Jules Payot, La faillite de l'enseignement, p.230, Librairie Félix Alcan, 1937.
Je relis beaucoup; je crois comprendre beaucoup mieux. C'est une vieillesse qui n'est pas sans charme que celle que l'on consacre à corriger ses vieux contresens.
Émile Faguet, L'art de lire, éd Armand Colin, p. 140.
Il n'y a pas de troubles mathématiques. Il n'y a que des enfants troublés.
Stella Baruk, Échec et maths, Éd. Seuil Points/S11.
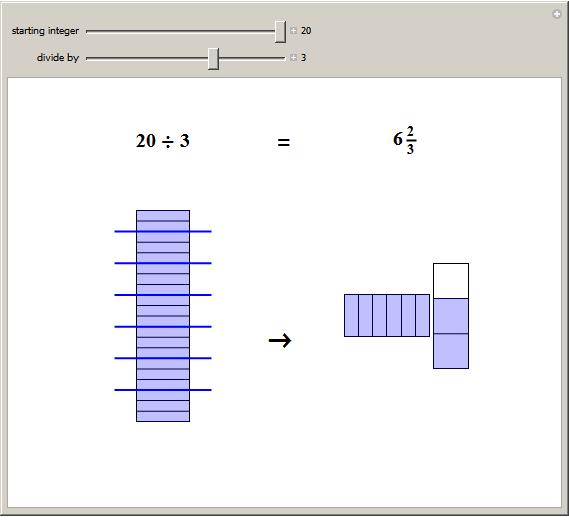
Mais...
Mais observez bien la figure. N’y trouvez-vous pas quelque chose... d’incompréhensible ?
Non ?
Alors peut-être cela vous sera-t-il plus évident à partir des images ci-dessous tirées du même fichier.
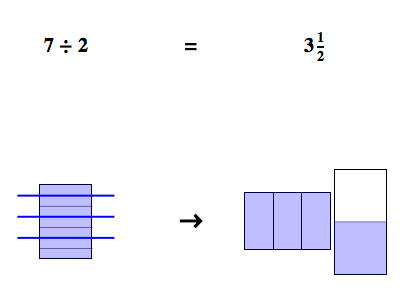
Fig. 2
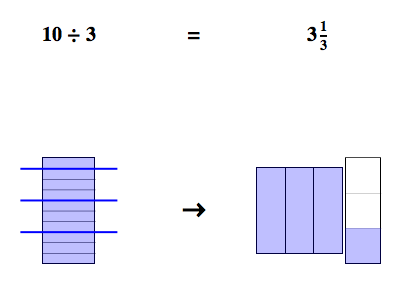
Fig. 3
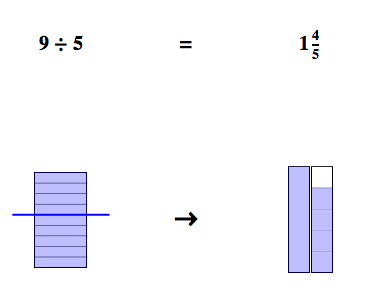
Fig. 4
Il faut vraiment faire attention avec ce qu’on trouve sur le web. Et toujours garder son esprit critique. Ce fichier se trouvant sur l’excellent (mais vraiment EXCELLENT) site de Mathematica, on pourrait s’attendre à n’y trouver que du matériel presque parfait. Ce n’est pas le cas ici. Mes explications :
Prenons la première image qui illustre la division de 20 par 3.
D’abord, n’oublions pas qu’on s’adresse ici à des élèves de niveau élémentaire. On serait fort tenté d’utiliser ce fichier comme support à l’enseignement. Mais, enseignant qui lisez ceci, n’en faites rien !!!
- Le contexte n’est pas donné. On sait que le symbole de division peut vouloir dire deux idées très différentes
- L’idée de partage dans le cas, par exemple, où 3 personnes désirent partager 20 pommes.
- L’idée de contenance. Par exemple : combien de paquets de trois pommes puis-je faire si j’ai 20 pommes ? Dans le cas qui nous intéresse ici, il s’agit clairement d’une division contenance, car on réalise des paquets de trois rectangles, paquets séparés par une ligne horizontale bleue. (Note : pour illustrer la division partage, on procéderait de la manière suivante : un petit rectangle à Paul, un petit rectangle à Pierre, un petit rectangle à Gilles, qu’on répéterait autant de fois que nécessaire.)
- Pour être «concret», l’auteur du fichier indique le nombre-de-fois par un rectangle bleu (l'aboutissement de mes flèches dans l'image). Un objet rectangle agit donc comme compteur-de-fois qu’on trouve 3 dans 20. Ce choix est didactiquement discutable. L’enfant pourrait facilement croire que partager 20 rectangles en paquet de trois rectangles a pour résultat des rectangles, alors que le résultat est un nombre de paquets de trois rectangles.
- Autre problème didactique qui m'apparaît plus grave. Que fait l’auteur avec les deux autres rectangles qui restent ? Tout semble indiquer qu’il transforme ça en deux tiers d’un nouveau rectangle dont les dimensions sont prises on ne sait trop où. Comment voulez-vous qu’un enfant y comprenne quelque chose : il n’y a rien, mais absolument rien de logiquement correct dans ce «report» de deux rectangles.
D’ailleurs, dans la division contenance, le reste doit rester un reste. Ici, on devrait avoir comme réponse : Je peux faire 6 paquets (illustrés par de petits rectangles à droite) et il me reste deux rectangles (rectangles qui n’ont aucun lien avec les rectangles de droite) avec lesquelles je ne peux faire de paquet. À la limite, sans doute pourrait-on dire : avec les deux rectangles qui restent, on peut remplir aux 2/3 un paquet de même dimension que les paquets précédents.
C’est ce que la fig.4 semble vouloir monter. Je peux faire un paquets de cinq rectangles et je remplis aux 4/5 un autre paquet. Mais cette explication est à la limite du pédagogiquement acceptable et, didactiquement parlant, à éviter. L'enfant voit des rectangles qui, à gauche représentent de vrais objets, et à droite des nombres-de-fois, et même une fraction de nombre-de-fois. N'est-ce pas ajouter de la confusion ?
En comparant toutes les images, un enfant un peu alerte pourrait nous demander, par exemple, ce qu’on fait avec le vide dans un paquet et pourquoi le paquet qui contienne les restes n'est pas toujours égal au paquet qui représente le nombre-de-fois. À mon avis, ces illustrations contribuent au petit côté magique des mathématiques où l’enfant sent qu’il n’y a rien à comprendre, que c’est comme ça, et c’est tout !
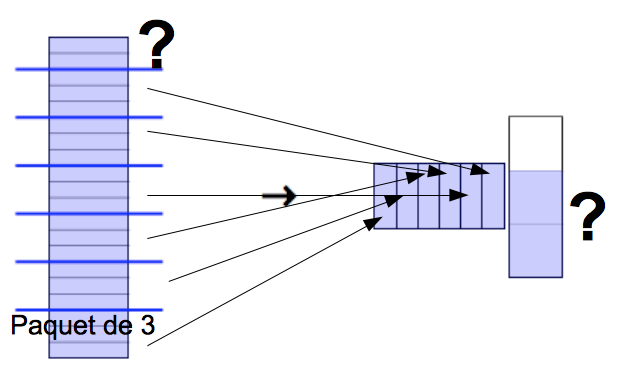 Fig. 2
Fig. 2
