Jobineries

Il peut arriver de tomber en amour avec un problème. Tel fut mon cas pour celui-ci :


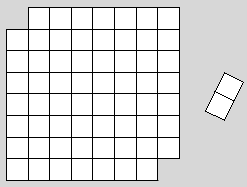
C'est un tableau de 8 cases sur 8 cases auquel on a retranché la case inférieure droite et la case supérieure gauche. Le problème est de démontrer qu'il est possible (ou impossible) de couvrir les 62 cases à l'aide de 31 dominos qui englobent eux-mêmes deux cases contiguës.

Si vous prenez le temps de construire le matériel pour faire vos propres essais, vous vous rendrez bien vite compte que la chose est loin d'être simple. Plus vous ferez des tentatives, plus vous serez persuadé qu'il est probablement impossible de remplir la condition. Or on cherche ici une preuve et non pas seulement une vague impression.

C'est là qu'entre toute la beauté d'un ingénieux HAHA. Le problème avec les intuitions géniales est qu'elles peuvent survenir en 10 secondes, en 10 jours, en 10 ans ou jamais... Je vais donc ici vous dévoiler ce HAHA.

Colorons alternativement les cases en blanc et noir.

Le tableau contient maintenant 30 cases blanches et 32 cases noires, puisque les deux cases de coin supprimées sont blanches. Or, les dominos couvrent nécessairement une case blanche et une case noire puisqu'ils couvrent des cases contiguës. Nous avons au total 31 dominos. Donc, en supposant qu'il soit possible de les placer, ils couvriront 31 cases blanches et 31 cases noires. Cela est donc impossible puisque nous n'avons que 30 cases blanches. CQFD.

Je crois profondément que même si vous détestez ce type de problèmes, vous ne pouvez qu'être estomaqué devant une telle démonstration du raisonnement humain. Cette solution est à mon avis d'une très grande beauté. Elle est simple, ingénieuse, brillante. Cette solution illustre la force de notre cerveau et je vois difficilement comment un superordinateur équipé d'une intelligence artificielle grandiose pourrait arriver à une telle solution. Mais s'il y arrivait, alors je donnerais certainement le statut de vivant à cette machine.

Revenons un peu sur le problème pour en tirer quelques observations.

1. Il est aculturel car aucune connaissance préalable n'est nécessaire;
2. Il est de la catégorie essaie-erreur où tous les essais seront ratés;
3. Il est extrêmement plate, et ne semble avoir aucune utilité pratique;
4. Son énoncé est très simple;
5. Il n'attirera probablement que peu de personnes.

Pour ma part jamais je ne demanderais à des élèves de le résoudre.

Cependant, je n'hésiterais pas un instant à le leur soumettre. Et après cinq minutes maximum d'essais, je leur balancerais la solution. Car, voyez-vous, le grand intérêt ici réside justement dans la beauté de sa solution, et dans les discussions qui risquent d'en découler. D'ailleurs, mon objectif serait de vérifier si les élèves sont capables d'apprécier une telle solution. (Pourquoi n'existe-t-il pas une compétence intitulée «Apprécier des oeuvres mathématiques»?) De plus, il est dans mes convictions très profondes qu'il faut montrer des centaines de problèmes et solutions aux élèves et tenter avec eux de dégager les caractéristiques de ces solutions de manière à ce qu'ils puissent construire une banque «expériencielle» de raisonnements mathématiques.

Mais au fait, qu'en est-il de cette solution?

1. Elle est extrêmement simple mais extrêmement difficile à trouver (HAHA!) ;
2. La solution consiste à ajouter des éléments qui n'y étaient pas (le noir et le blanc);
3. Les dominos sont aussi notés (blanc-noir);
4. Cette notation du problème a permis ensuite de le résoudre par simple raisonnement arithmétique.

Lorsque j'ai lu ce billet de François Guité sur la beauté, j'ai immédiatement pensé à ce problème dont la solution m'épate toujours autant.